Richiami di Calcolo Combinatorio
Il calcolo combinatorio ha come scopo principale il conteggio del numero di modi in cui possono verificarsi determinati eventi, senza doverli enumerare uno per uno. Questo permette di risolvere problemi legati alla disposizione, alla scelta e alla distribuzione di oggetti in modo efficiente e rigoroso.
Un modello efficace per affrontare queste situazioni è quello delle \(n\) scatole numerate e delle \(k\) palline, che permette di classificare i problemi combinatori in base a due aspetti fondamentali:
1. Le palline possono essere numerate (distinguibili) o non numerate (indistinguibili).
2. Il numero di scatole rispetto alle palline determina se tutte possono essere sistemate senza vincoli o se vi è un limite.
A partire da questa impostazione, si sviluppano le formule fondamentali della combinatoria, che trovano applicazioni in statistica, probabilità e molte altre discipline.
Quando ogni scatola può contenere al massimo una pallina, si individuano quattro casi principali, ciascuno con una specifica formula combinatoria.
Scelte indipendenti con ripetizione: \(k^n\)
Si consideri il caso in cui abbiamo \(k\) palline numerate e ogni pallina può essere collocata indipendentemente in una qualsiasi delle \(n\) scatole disponibili, senza restrizioni sul numero di volte in cui una scatola può essere scelta.
Il numero totale di distribuzioni è dato da:
\[ n^k \]
che rappresenta il numero di sequenze ordinate di \(n\) elementi scelti tra \(k\) possibilità.
Esempio 19.7 (Valigetta) Un sistema di sicurezza utilizza un codice a tre cifre, in cui ciascun numero può variare da 1 a 9. Il codice è quindi una sequenza ordinata di tre elementi, scelti tra 9 possibilità:
\[ 9^3 = 729 \]
Esistono 729 possibili codici di apertura.
\(n = k\) Palline numerate: permutazioni
Quando il numero di palline è uguale al numero di scatole e ogni pallina è distinguibile, il problema diventa quello di ordinare \(n\) elementi distinti. Il numero di modi in cui ciò è possibile è dato dal fattoriale.
Sia \(n\in\mathbb{N}\) un numero naturale, si definisce \(n\) fattoriale, il numero
\[n!=n(n-1)(n-2)...3\cdot 2 \cdot 1\]
conta in quanti modo posso rimescolare \(n\) oggetti.
Nota. Per definizione \(0!=1\)
In figura \(3!\).
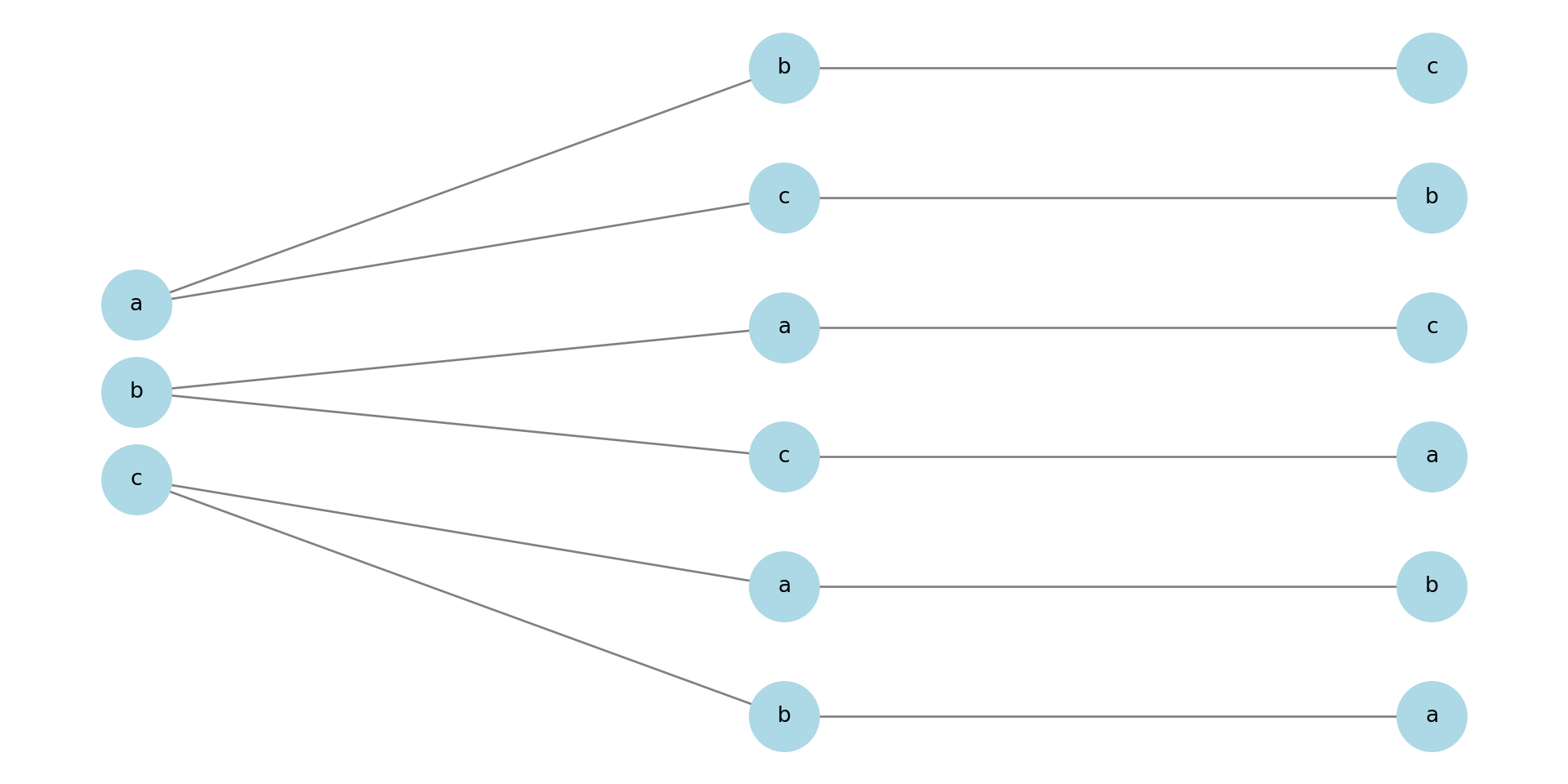
Esempio 19.8 \(3!=3\cdot 2\cdot 1=6\), \(10!=10\cdot 9\cdot... \cdot1 =3628800\)
Esempio 19.9 (Mazzo di Carte) Consideriamo un mazzo di 52 carte tutte distinte. Il numero di modi in cui il mazzo può essere mescolato corrisponde a tutte le possibili permutazioni delle 52 carte:
\[ 52! = \scriptsize 80\hspace{0.9pt}658\hspace{0.9pt}175\hspace{0.9pt}170\hspace{0.9pt}944\hspace{0.9pt}942\hspace{0.9pt}408\hspace{0.9pt}940\hspace{0.9pt}349\hspace{0.9pt}866\hspace{0.9pt}698\hspace{0.9pt}506\hspace{0.9pt}766\hspace{0.9pt}127\hspace{0.9pt}860\hspace{0.9pt}028\hspace{0.9pt}660\hspace{0.9pt}283\hspace{0.9pt}290\hspace{0.9pt}685\hspace{0.9pt}487\hspace{0.9pt}972\hspace{0.9pt}352 \]
che è un numero estremamente grande, pari a circa \(8.0658 \times 10^{67}\). Questo valore evidenzia come, ogni volta che un mazzo di carte viene mescolato, sia altamente improbabile che l’ordine ottenuto sia mai stato realizzato prima.
\(n > k\) Palline numerate: disposizioni senza ripetizione
Se \(n\) è maggiore di \(k\) e le palline sono numerate, il problema diventa quello di scegliere \(k\) elementi distinti da un insieme di \(n\) e disporli in un ordine specifico. In questo caso, la formula è:
\[ \frac{n!}{(n-k)!} \]
che rappresenta il numero di sequenze ordinate di \(k\) elementi scelti da un insieme di \(n\) elementi distinti.
Esempio 19.10 Se si estrae una mano di 5 carte da un mazzo di 52 e si considera l’ordine di estrazione, il numero di possibili sequenze è:
\[ \frac{52!}{(52-5)!} = \frac{52!}{47!} \]
che fornisce \(311\,875\,200\) possibili sequenze.
\(n > k\) Palline non numerate: coefficienti binomiale
Se \(n > k\) e le palline sono non numerate, il problema si riduce alla scelta di \(k\) scatole tra \(n\) disponibili, senza considerare l’ordine. Questo corrisponde al numero di combinazioni di \(k\) elementi scelti tra \(n\), dato dal coefficiente binomiale:
\[ \binom{n}{k} = \frac{n!}{k!(n-k)!} \]
Esempio 19.11 (Sei al super enalotto) Nel Superenalotto, si scelgono 6 numeri tra 90, senza che l’ordine abbia rilevanza. Il numero totale di combinazioni possibili è:
\[ \binom{90}{6} = \frac{90!}{6!(90-6)!} = \frac{90!}{6!84!} \]
che fornisce \(622\,614\,630\) possibilità. Questo spiega l’estrema difficoltà di vincere il jackpot.
Il coefficiente binomiale
Il coefficiente binomiale \(\binom{n}{k}\) conta in quanti modi posso disporre \(k\) oggetti indistinguibili in \(n\ge k\) posti: \[\binom{n}{ k}=\frac {n!}{k!(n-k)!}\]
Proprietà utili
\[\begin{eqnarray*} \binom{n}{ k} &=&\binom{n}{ n-k},\qquad\text{Per esempio:} \\ \binom{5}{ 3} &=&\binom{5}{ 2}=10,\\ \binom{n}{ 0} &=&\binom{n}{ n} = 1 \\ \binom{n}{ 1} &=&\binom{n}{ n-1}=n \\ \binom{n}{ k} &=&\binom{n-1}{k-1}+\binom{n-1}{k} \end{eqnarray*}\]
In matematica \(\binom{n}{ k}\) è il \(k\)-esimo elemento della \(n\)-esima riga del triangolo di Tartaglia.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | |||||||
| 1 | 1 | 1 | ||||||
| 2 | 1 | 2 | 1 | |||||
| 3 | 1 | 3 | 3 | 1 | ||||
| 4 | 1 | 4 | 6 | 4 | 1 | |||
| 5 | 1 | 5 | 10 | 10 | 5 | 1 | ||
| 6 | 1 | 6 | 15 | 20 | 15 | 6 | 1 | |
| 7 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 |