Capitolo 11 Elementi di Teoria della Stima
Il problema della stima nasce quando si vuole assegnare un valore numerico a una quantità incognita, chiamata parametro, a partire da un insieme limitato di osservazioni. In statistica, questa operazione si fonda sull’idea che i dati provengano da un meccanismo aleatorio e che il parametro rappresenti una proprietà stabile della popolazione o del modello da cui i dati sono stati generati.
Nel nostro contesto, un parametro può essere, ad esempio, la media \(\mu\), la varianza \(\sigma^2\), una proporzione \(\pi\), un tasso \(\lambda\), o più in generale un elemento \(\theta\) di uno spazio dei parametri \(\Theta\). La stima si basa sull’uso di un campione, ossia un insieme di dati osservati, che contiene informazione parziale sulla popolazione o sul modello.
11.1 Campionamento
Un campione casuale è un certo numero di \(n\) di osservazioni prese a caso dalla popolazione \(\mathscr{P}\). Nel quadro dell’inferenza statistica, il campionamento è il processo attraverso cui si seleziona un sottoinsieme di unità da una popolazione \(\mathscr{P}\), al fine di trarne informazioni utili. Il tipo di inferenza che si può condurre dipende in larga parte dal modo in cui è stato ottenuto il campione.
11.1.1 Campioni casuali
Nel nostro percorso considereremo due situazioni fondamentali:
- Il campionamento con reinserimento (o con restituzione), dove ogni osservazione è estratta in modo indipendente dalla popolazione o dal modello.
- Il campionamento senza reinserimento, dove le osservazioni non sono indipendenti e provengono da una popolazione finita di dimensione \(N\), da cui vengono estratti \(n\) elementi senza ripetizioni.
Nel primo caso, \(X_1, ..., X_n\) sono IID (indipendenti e identicamente distribuite) e rappresentano il caso classico di inferenza da popolazioni infinite o da modelli. Nel secondo, si ha una struttura di dipendenza debole tra le unità campionarie, e l’inferenza deve tener conto della dimensione della popolazione e della frazione di campionamento \(n/N\).
11.1.2 Lessico
Un campione in essere (prima di essere osservato) è una sequenza di VC \[X_1,...,X_n\]
un campione osservato è un insieme di numeri \[\mathbf{x}=(x_1,...,x_n)\]
Lo Spazio dei Campioni \(\mathcal{S}\) è il supporto della VC multipla \(X_1,...,X_n\) è l’insieme di tutti i possibili campioni di ampiezza \(n\): \((x_1,...,x_n)\) che possiamo osservare.
11.1.3 Esempio al finito
Si dispone di un’urna contente 4 bussolotti \[\{0,1,3,7\}\]
\[\begin{eqnarray*} \mu &=& E(X_i) = \sum_{x\in S_X}x P(X=x)\\ &=& 0 \frac { 1 }{ 4 }+ 1 \frac { 1 }{ 4 }+ 3 \frac { 1 }{ 4 }+ 7 \frac { 1 }{ 4 } \\ &=& 2.75 \\ \sigma^2 &=& V(X_i) = \sum_{x\in S_X}x^2 P(X=x)-\mu^2\\ &=&\left( 0 ^2\frac { 1 }{ 4 }+ 1 ^2\frac { 1 }{ 4 }+ 3 ^2\frac { 1 }{ 4 }+ 7 ^2\frac { 1 }{ 4 } \right)-( 2.75 )^2\\ &=& 7.188 \end{eqnarray*}\]
Se estraiamo \(n=2\) volte Senza Reinserimento, lo spazio dei campioni è di dimensione \(\#\mathcal{S}=4\times 3\) ed è descritto in tabella (11.1).
| \(0\) ; \(\color{blue}{1/3}\) | \(1\) ; \(\color{blue}{1/3}\) | \(3\) ; \(\color{blue}{1/3}\) | \(7\) ; \(\color{blue}{1/3}\) | |
|---|---|---|---|---|
| \(0\) ; \(\color{blue}{1/4}\) |
|
\((0,1)\) ; \(\color{red}{1/12}\) | \((0,3)\) ; \(\color{red}{1/12}\) | \((0,7)\) ; \(\color{red}{1/12}\) |
| \(1\) ; \(\color{blue}{1/4}\) | \((1,0)\) ; \(\color{red}{1/12}\) |
|
\((1,3)\) ; \(\color{red}{1/12}\) | \((1,7)\) ; \(\color{red}{1/12}\) |
| \(3\) ; \(\color{blue}{1/4}\) | \((3,0)\) ; \(\color{red}{1/12}\) | \((3,1)\) ; \(\color{red}{1/12}\) |
|
\((3,7)\) ; \(\color{red}{1/12}\) |
| \(7\) ; \(\color{blue}{1/4}\) | \((7,0)\) ; \(\color{red}{1/12}\) | \((7,1)\) ; \(\color{red}{1/12}\) | \((7,3)\) ; \(\color{red}{1/12}\) |
|
Se invece estraiamo CR, lo spazio dei campioni è di dimensione \(\#\mathcal{S}=4^2=16\) ed è descritto in tabella (11.2).
| \(0\) ; \(\color{blue}{1/4}\) | \(1\) ; \(\color{blue}{1/4}\) | \(3\) ; \(\color{blue}{1/4}\) | \(7\) ; \(\color{blue}{1/4}\) | |
|---|---|---|---|---|
| \(0\) ; \(\color{blue}{1/4}\) | \((0,0)\) ; \(\color{red}{1/16}\) | \((0,1)\) ; \(\color{red}{1/16}\) | \((0,3)\) ; \(\color{red}{1/16}\) | \((0,7)\) ; \(\color{red}{1/16}\) |
| \(1\) ; \(\color{blue}{1/4}\) | \((1,0)\) ; \(\color{red}{1/16}\) | \((1,1)\) ; \(\color{red}{1/16}\) | \((1,3)\) ; \(\color{red}{1/16}\) | \((1,7)\) ; \(\color{red}{1/16}\) |
| \(3\) ; \(\color{blue}{1/4}\) | \((3,0)\) ; \(\color{red}{1/16}\) | \((3,1)\) ; \(\color{red}{1/16}\) | \((3,3)\) ; \(\color{red}{1/16}\) | \((3,7)\) ; \(\color{red}{1/16}\) |
| \(7\) ; \(\color{blue}{1/4}\) | \((7,0)\) ; \(\color{red}{1/16}\) | \((7,1)\) ; \(\color{red}{1/16}\) | \((7,3)\) ; \(\color{red}{1/16}\) | \((7,7)\) ; \(\color{red}{1/16}\) |
11.2 Il Modello Statistico
Un modello statistico descrive formalmente il processo che ha generato i dati osservati. È composto da due elementi principali:
- un modello probabilistico, che specifica la distribuzione delle osservazioni in funzione di uno o più parametri incogniti;
- un piano di campionamento, che determina le modalità con cui le osservazioni sono state ottenute dalla popolazione di riferimento.
In queste pagine assumeremo sempre che le osservazioni \(X_1, ..., X_n\) siano indipendenti e identicamente distribuite (IID), ossia ottenute tramite campionamento casuale semplice con reinserimento. Questo tipo di campionamento è coerente con l’ipotesi che ogni unità del campione sia stata estratta in modo indipendente, e che tutte le unità della popolazione abbiano la stessa probabilità di essere selezionate.
Nel nostro contesto, il modello probabilistico scriveremo con \(X_1,..,X_n\), \(n\) VC IID, replicazioni della stessa variabile \(X\sim\mathscr{L}(\theta)\), \(\theta\in\Theta\) \[ X_i \sim \mathscr{L}(\theta),\forall i=1,...,n \qquad \theta \in \Theta, \] dove \(\mathscr{L}(\theta)\) è una famiglia di distribuzioni parametrica e \(\theta\) è il parametro (o vettore di parametri) che descrive la popolazione e \(\Theta\) lo spazio in cui \(\theta\) è definito.
Useremo le lettere greche per i parametri (incogniti) della popolazione e lettere latine per le osservazioni.
11.2.1 Esempi
- \(X_i \sim \text{Ber}(\pi)\), con \(\pi \in [0,1]\): modello per variabili dicotomiche, adatto per rappresentare esiti binari (successo/insuccesso). In questo caso \(\theta\equiv\pi\) e \(\Theta\equiv [0,1]\).
- \(X_i \sim \text{Pois}(\lambda)\), con \(\lambda \in \mathbb{R}^+\): modello per conteggi, adatto a descrivere eventi rari su un intervallo fissato. In questo caso \(\theta\equiv\lambda\) e \(\Theta\equiv \mathbb{R}^+\).
- \(X_i \sim N(\mu, \sigma^2)\), con \(\mu \in \mathbb{R}, \sigma^2 \in \mathbb{R}^+\): modello per variabili continue, con distribuzione simmetrica e forma a campana. In questo caso \(\theta\equiv(\mu,\sigma^2)\) e \(\Theta\equiv \mathbb{R}\times\mathbb{R}^+\).
- \(X_i \sim \mathscr{L}(\theta)\): notazione generica per una famiglia distribuzionale qualsiasi, dove \(\theta \in \Theta\) rappresenta i parametri che vogliamo stimare.
Nel paradigma classico la probabilità si assegna alle \(X_i\), in quanto risultato di un sorteggio casuale \[P(X_1,...,X_n;\theta)\]
Ma non è consentito trattare con lo strumento della probabilità l’incertezza sul parametro \(\theta\) che governa la popolazione. Perché \(\theta\) è incognito ma non è il frutto di una selezione casuale.
Nel paradigma Bayesiano l’incertezza sul parametro viene trattata con gli stessi strumenti dell’incertezza sui dati, dando vita ad un teoria coerente e molto utile per alcune applicazioni particolari.
11.2.2 Scopo del modello
L’obiettivo dell’inferenza statistica è trarre conclusioni sul parametro \(\theta\), sulla base del campione osservato \(\mathbf{x} = (x_1, ..., x_n)\). Lo stesso campione può essere interpretato in modo diverso a seconda del modello adottato: per questo, esplicitare il modello è sempre il primo passo di un’analisi statistica. Perfetto, possiamo riformulare e ampliare il paragrafo sul campionamento, tenendo conto della necessità di collegarlo bene al discorso sull’inferenza e sul modello statistico. Ti propongo una bozza con tono sobrio e coerente con il resto del libro:
11.3 Gli stimatori
Stimare, in statistica, significa scegliere un punto (stima puntuale) o una regione (stima intervallare) dello spazio dei parametri \(\Theta\) alla luce dei dati \(x_1,...,x_n\).
Uno stimatore puntuale (point estimator) è una statistica \(\hat\theta\) che trasforma il campione \(X_1,...,X_n\) in un punto dello spazio dei parametri: \[\hat\theta:\mathcal{S}\to\Theta\]
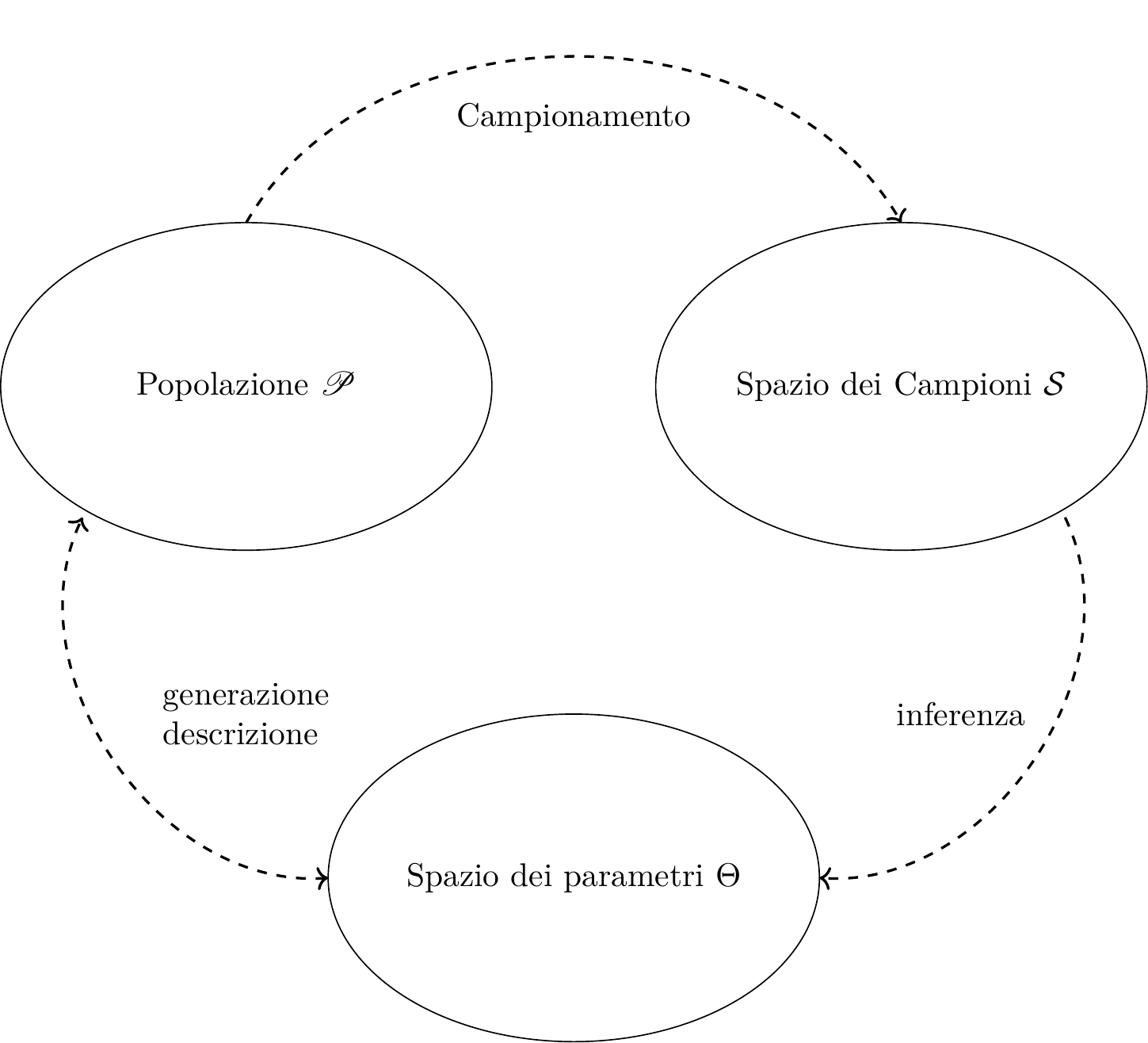
Figura 11.1: Schema concettuale dell’inferenza statistica
Il campione \(X_1,...,X_n\) casuale viene trasformato attraverso \(\hat\theta\) in un punto specifico di \(\Theta\) \[\hat\theta(X_1,...,X_n)=\hat\theta\in\Theta\]
Uno stimatore è una variabile casuale in quanto funzione di valori casuali.
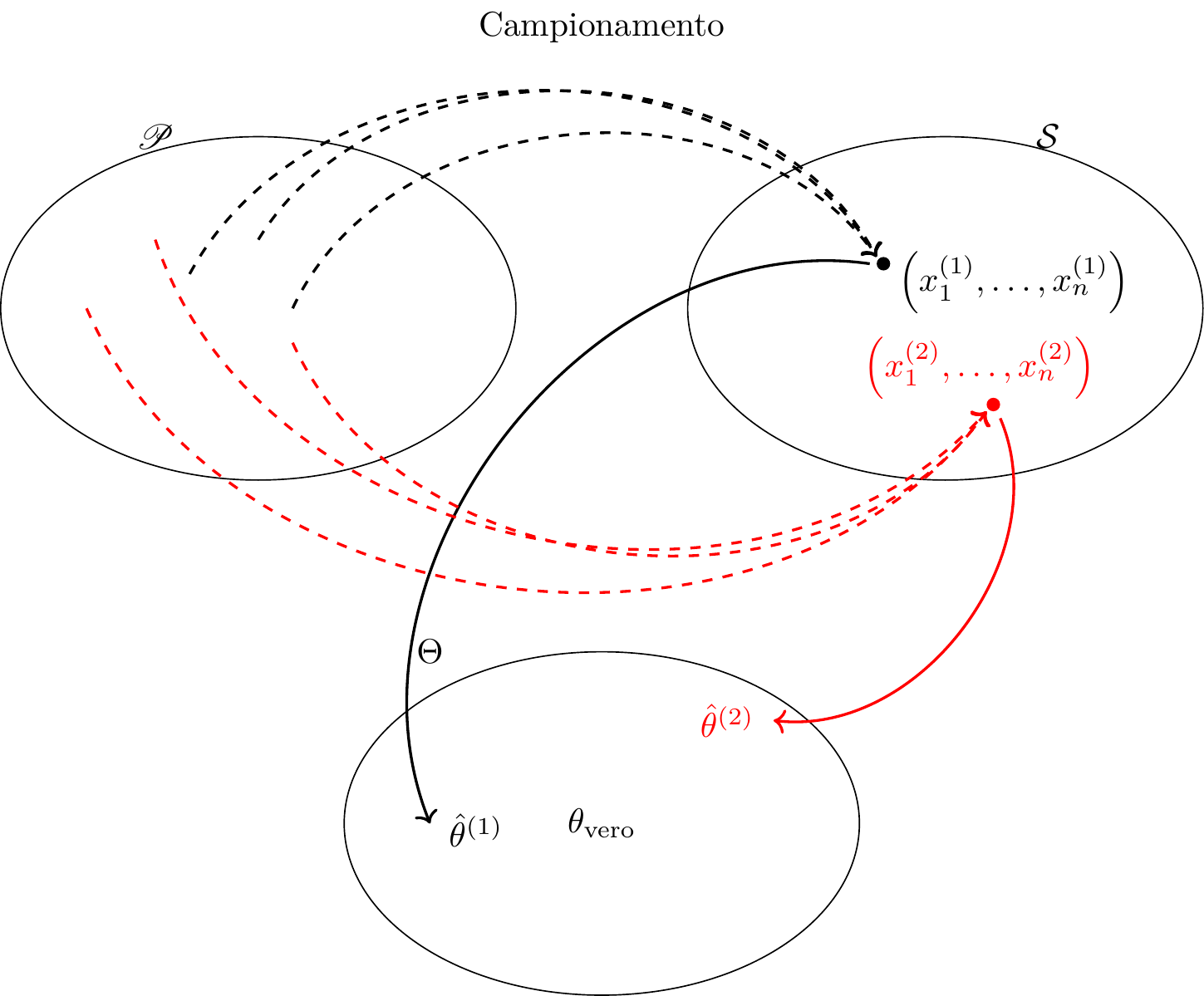
Figura 11.2: Ogni campione è un punto nello spazio dei campioni, ad ogni campione corrisponde una stima nello spazio dei parametri
Esempio 11.1 Da una popolazione che ha \(E(X_i)=\mu\) incognita, potremmo proporre di stimare \(\mu\) con la media dei dati che otterremo: \[\hat\mu(X_1,...,X_n)=\frac 1 n \sum_{i=1}^n X_i=\bar X=\hat \mu\]
Esempio 11.2 Da una popolazione di Poisson che ha \(X_i\sim\text{Poiss}(\lambda)\), \(\lambda\) incognita, potremmo proporre di stimare \(\lambda\) con la mediana dei dati che otterremo: \[\hat\lambda(X_1,...,X_n)=X_{0,5}=\hat\lambda\]
11.3.1 Stimatori e Stime
- Uno Stimatore: \(\hat\theta=\hat\theta(X_1,...,X_n)\) è funzione di \(X_1,...,X_n\) è una VC
- Una Stima: \(\hat\theta_\text{obs}=\hat\theta(x_1,...,x_n)\) è funzione di \(x_1,...,x_n\) e dunque è un numero
Esempio 11.3 Lanciamo una moneta e non sappiamo se è bilanciata, cioè \(\pi\), la probabilità di ottenere testa, è incognita, potremmo proporre di stimare \(\pi\) con la proporzione dei dati e otterremo: \[ \hat \pi(X_1,...,X_n)=\frac {S_n} n =\hat\pi \]
Estraiamo \(n=5\) individui dalla popolazione \(x_1=0\), \(x_2=1\), \(x_3=0\), \(x_4=1\), \(x_5=1\),
Per ottenere \(\hat\mu\) la stima di \(\mu\) applichiamo \(\hat\theta\) ai dati e otteniamo \[ \hat\pi_\text{obs}=\hat\pi(0,1,0,1,1) = \frac 3 5=0.6 \]
Esempio 11.4 Da una popolazione che ha \(E(X_i)=\mu\) incognita, potremmo proporre di stimare \(\mu\) con la media dei dati che otterremo: \[\hat \mu(X_1,...,X_n)=\frac 1 n \sum_{i=1}^n X_i=\hat \mu\]
Estraiamo \(n=5\) individui dalla popolazione \(x_1=2.1\), \(x_2=2.4\), \(x_3=3.2\), \(x_4=1.7\), \(x_5=3.0\),
Per ottenere \(\hat\mu\) la stima di \(\mu\) applichiamo \(\hat\theta\) ai dati e otteniamo \[ \hat\mu_\text{obs}=\hat\mu(2.1,2.4,3.2,7.1,3.0) = \frac 1 5\sum_{i=1}^5x_i=\frac 1 5 17.8=3.56 \]
Esempio 11.5 Da una popolazione di Poisson che ha \(X_i\sim\text{Poiss}(\lambda)\), \(\lambda\) incognita, potremmo proporre di stimare \(\lambda\) con la mediana dei dati che otterremo: \[\hat\lambda(X_1,...,X_n)=X_{0,5}=\hat\lambda\]
Osserviamo \(n=7\) valori (già riordinati)
\(x_{(1)}=0\), \(x_{(2)}=0\), \(x_{(3)}=2\), \(x_{(4)}=2\), \(x_{(5)}=3\), \(x_{(6)}=4\), \(x_{(7)}=7\),
Per ottenere \(\hat\lambda\) la stima di \(\lambda\) applichiamo \(\hat\theta\) ai dati e otteniamo \[ \hat\lambda(x_1,...,x_7) = x_{0.5}=x_{(4)}=2 \]
11.3.2 Come scegliere uno stimatore
La definizione non offre un criterio per la scelta. Gli stimatori vengono costruiti per avere la miglior precisione possibile. La precisione non si può valutare sulla singola stima ma studiando, prima di osservare i dati, le proprietà probabilistiche dello stimatore.
Le proprietà auspicabili per uno stimatore sono di due tipi
- Esatte (per \(n\) finito)
- Asintotiche (per \(n\) che diverge)
11.3.3 Proprietà Auspicabili di uno stimatore (per \(n\) finito)
Uno stimatore si dice corretto (unbiased) se in media cade sul parametro vero.
Definizione 11.1 (Correttezza di uno stimatore) Siano \(X_1,...,X_n\), \(n\) VC, IID, replicazioni della stessa \(X\sim\mathscr{L}(\theta)\), sia \(\hat\theta\) uno stimatore per \(\theta\). Lo stimatore \(\hat\theta\) si dice corretto se \[ E(\hat\theta(X_1,...,X_n))=E(\hat\theta)=\theta \]
La misura dell’errore di stima è data dalla distanza quadratica media delle stime dal valore vero.
Definizione 11.2 (Mean Squared Error di uno stimatore) Si definisce Errore Quadratico Medio (Mean Squared Error) la quantità \[MSE(\hat\theta)=E((\hat\theta-\theta)^2)=V(\hat\theta)+B^2(\hat\theta)\] dove \[B(\hat\theta)=|E(\hat\theta)-\theta|\]
Se lo stimatore è corretto allora il \(MSE\) coincide con la varianza dello stimatore.
se \(\hat\theta\) è corretto allora \[MSE(\hat\theta)=V(\hat\theta)\]
L’efficienza è una quantità teorica che dipende da quantità incognite, ma il suo calcolo teorico può essere utilizzato per confrontare diversi stimatori.
Definizione 11.3 (Efficienza di uno stimatore) Siano \(\hat\theta_1\) e \(\hat\theta_2\) due stimatori per \(\theta\), si dice che \(\hat\theta_1\) è più efficiente di \(\hat\theta_2\) se e solo se \[MSE(\hat\theta_1)<MSE(\hat\theta_2)\]
Se \(\hat\theta_1\) e \(\hat\theta_2\) sono entrambi corretti, allora, \(\hat\theta_1\) è più efficiente di \(\hat\theta_2\) se e solo se \[V(\hat\theta_1)<V(\hat\theta_2)\]
L’errore di uno stimatore è l’inverso della sua precisione.
11.3.4 Media aritmetica e varianza campionaria caso IID
Siano \(X_1,...,X_n\), \(n\) VC, IID, replicazioni della stessa \(X\) tale che \(E(X)=\mu\) e \(V(X)=\sigma^2\), sia \(\hat\theta\equiv\hat \mu\) uno stimatore per \(\mu\) \[ \hat \mu=\bar X=\frac 1 n \sum_{i=1}^n X_i \]
Dai risultati che già conosciamo sappiamo che \[ E(\hat \mu)=\mu \] e dunque \(\hat \mu\) è sempre uno stimatore corretto per \(\mu\). Essendo \(\hat \mu\) corretto per \(\mu\) allora \[MSE(\hat \mu)=V(\hat \mu)=\frac{\sigma^2}n\]
Si consideri la varianza campionaria: \[ \hat\sigma^2=\frac 1 n \sum_{i=1}^n(X_i-\hat \mu)^2 \]
Si può dimostrare che
\[ E(\hat \sigma^2)=\frac {n-1}n \sigma^2<\sigma^2 \]
11.3.5 Media aritmetica campionamento SR (popolazioni finite)
Siano \(X_1,...,X_n\), \(n\) VC, osservazioni estratte SR da una popolazione \(X\) di \(N\) individui, tale che \(E(X)=\mu\) e \(V(X)=\sigma^2\), sia \(\hat\theta\equiv\hat \mu\) uno stimatore per \(\mu\) \[ \hat \mu=\frac 1 n \sum_{i=1}^n X_i \] Allora \[ E(\hat \mu)=\mu \] e dunque \(\hat \mu\) è sempre uno stimatore corretto per \(\mu\). Essendo \(\hat \mu\) corretto per \(\mu\) allora \[MSE(\hat \mu)=V(\hat \mu)\]
Per calcolare \(V(\hat \mu)\) dobbiamo tenere conto della frazione di campionamento \(n/N\)
\[ MSE(\hat \mu)=\frac{N-n}{N-1}\frac{\sigma^2} n \]
dove \(\frac{N-n}{N-1}\) è chiamato coefficiente di correzione per popolazioni finite. Osserviamo che più alto è \(n\) più il coefficiente tende ad 1. Se \(n = N\) il coefficiente diventa zero il campione è diventato l’intera popolazione e l’incertezza sulla media è zero.
11.3.6 Esempio al finito
Riprendiamo il nostro esempio al finito con una popolazione di \(N=4\) \[\{0,1,3,7\}\]
\[\begin{eqnarray*} \mu &=& E(X_i) = \sum_{x\in S_X}x P(X=x)\\ &=& 0 \frac { 1 }{ 4 }+ 1 \frac { 1 }{ 4 }+ 3 \frac { 1 }{ 4 }+ 7 \frac { 1 }{ 4 } \\ &=& 2.75 \\ \sigma^2 &=& V(X_i) = \sum_{x\in S_X}x^2 P(X=x)-\mu^2\\ &=&\left( 0 ^2\frac { 1 }{ 4 }+ 1 ^2\frac { 1 }{ 4 }+ 3 ^2\frac { 1 }{ 4 }+ 7 ^2\frac { 1 }{ 4 } \right)-( 2.75 )^2\\ &=& 7.188 \end{eqnarray*}\]
Se estraiamo \(n=2\) volte Senza Reinserimento, lo spazio dei campioni è di dimensione \(\#\mathcal{S}=4\times 3\) ed è descritto in tabella (11.1). Qui scegliamo
\[ \hat\mu = \frac{1}{2}(X_1+X_2) \]
In tabella (11.3) la distribuzione della VC media aritmetica campionaria.
| \(0\) ; \(\color{blue}{1/3}\) | \(1\) ; \(\color{blue}{1/3}\) | \(3\) ; \(\color{blue}{1/3}\) | \(7\) ; \(\color{blue}{1/3}\) | |
|---|---|---|---|---|
| \(0\) ; \(\color{blue}{1/4}\) |
|
\(0.5\) ; \(\color{red}{1/12}\) | \(1.5\) ; \(\color{red}{1/12}\) | \(3.5\) ; \(\color{red}{1/12}\) |
| \(1\) ; \(\color{blue}{1/4}\) | \(0.5\) ; \(\color{red}{1/12}\) |
|
\(2\) ; \(\color{red}{1/12}\) | \(4\) ; \(\color{red}{1/12}\) |
| \(3\) ; \(\color{blue}{1/4}\) | \(1.5\) ; \(\color{red}{1/12}\) | \(2\) ; \(\color{red}{1/12}\) |
|
\(5\) ; \(\color{red}{1/12}\) |
| \(7\) ; \(\color{blue}{1/4}\) | \(3.5\) ; \(\color{red}{1/12}\) | \(4\) ; \(\color{red}{1/12}\) | \(5\) ; \(\color{red}{1/12}\) |
|
Ricaviamo la distribuzione di \(\hat\mu\)
\[ \begin{array}{r|rrrrrr} \hat\mu& 0.5 & 1.5 & 2 & 3.5 & 4 & 5 \\ \hline P(\hat\mu) & \frac{2}{12} & \frac{2}{12} & \frac{2}{12} & \frac{2}{12} & \frac{2}{12} & \frac{2}{12} \\ \end{array} \]
il suo valore atteso
\[ E(\hat\mu) = \frac{2}{12} \cdot (0.5 + 1.5 + 2 + 3.5 + 4 + 5) = \frac{16.5}{6} = 2.75 = \mu \]
lo stimatore è corretto. Ricaviamo il suo MSE
\[\begin{eqnarray*} MSE(\hat\mu) &=& V(\hat\mu) + B^2(\hat\mu) \\ &=& V(\hat\mu) \qquad \text{in virtù della correttezza} \\ &=& \left( 0.5 ^2\frac { 1 }{ 6 }+ 1.5 ^2\frac { 1 }{ 6 }+ 2 ^2\frac { 1 }{ 6 }+ \right.\\ & & \left. + 3.5 ^2\frac { 1 }{ 6 }+ 4 ^2\frac { 1 }{ 6 }+ 5 ^2\frac { 1 }{ 6 } \right)-( 2.75 )^2\\ &=& 2.3958\\ &=& \frac{4-2}{4-1}\frac{7.1875}{2}\\ &=& \frac{N-n}{N-1}\frac{\sigma^2} n \end{eqnarray*}\]
Se estraiamo \(n=2\) volte con reinserimento, lo spazio dei campioni è di dimensione \(\#\mathcal{S} = 4 \times 4\) ed è descritto in tabella (11.2). Anche qui scegliamo:
\[ \hat\mu = \frac{1}{2}(X_1 + X_2) \]
In tabella qui sotto è riportata la distribuzione della variabile casuale media aritmetica campionaria.
\[ \begin{array}{ r|rrrrrrrr } & 0 ;&\color{blue}{ \frac{ 1 } { 4 }} & 1 ;&\color{blue}{ \frac{ 1 } { 4 }} & 3 ;&\color{blue}{ \frac{ 1 } { 4 }} & 7 ;&\color{blue}{ \frac{ 1 } { 4 }} \\ \hline 0 ;\color{blue}{ 1 / 4 }& 0;&\color{red}{\frac{1}{16}}& 0.5;&\color{red}{\frac{1}{16}}& 1.5;&\color{red}{\frac{1}{16}}& 3.5;&\color{red}{\frac{1}{16}}\\ 1 ;\color{blue}{ 1 / 4 }& 0.5;&\color{red}{\frac{1}{16}}& 1;&\color{red}{\frac{1}{16}}& 2;&\color{red}{\frac{1}{16}}& 4;&\color{red}{\frac{1}{16}}\\ 3 ;\color{blue}{ 1 / 4 }& 1.5;&\color{red}{\frac{1}{16}}& 2;&\color{red}{\frac{1}{16}}& 3;&\color{red}{\frac{1}{16}}& 5;&\color{red}{\frac{1}{16}}\\ 7 ;\color{blue}{ 1 / 4 }& 3.5;&\color{red}{\frac{1}{16}}& 4;&\color{red}{\frac{1}{16}}& 5;&\color{red}{\frac{1}{16}}& 7;&\color{red}{\frac{1}{16}}\\ \end{array} \]
E ricaviamo la distribuzione di, \(\hat\mu\)
\[ \begin{array}{ r|rrrrrrrrrr } \hat\mu & 0& 0.5& 1& 1.5& 2& 3& 3.5& 4& 5& 7 \\ \hline P( \hat\mu ) & \frac{1}{16}& \frac{2}{16}& \frac{1}{16}& \frac{2}{16}& \frac{2}{16}& \frac{1}{16}& \frac{2}{16}& \frac{2}{16}& \frac{2}{16}& \frac{1}{16} \\ \end{array} \]
Calcoliamo valore atteso e MSE.
\[\begin{eqnarray*} E(\hat\mu) &=& \sum_{\hat\mu}\hat\mu P(\hat\mu)\\ &=& 0 \frac { 1 }{ 16 }+ 0.5 \frac { 2 }{ 16 }+ 1 \frac { 1 }{ 16 }+ 1.5 \frac { 2 }{ 16 }+ 2 \frac { 2 }{ 16 }+ \\ & & +3 \frac { 1 }{ 16 }+ 3.5 \frac { 2 }{ 16 }+ 4 \frac { 2 }{ 16 }+ 5 \frac { 2 }{ 16 }+ 7 \frac { 1 }{ 16 } \\ &=& 2.75 = \mu \qquad\text{lo stimatore è corretto} \\ MSE(\hat\mu) &=& V(\hat\mu) + B^2(\hat\mu)\\ &=& V(\hat\mu)\\ &=&\left( 0 ^2\frac { 1 }{ 16 }+ 0.5 ^2\frac { 2 }{ 16 }+ 1 ^2\frac { 1 }{ 16 }+ 1.5 ^2\frac { 2 }{ 16 }+ 2 ^2\frac { 2 }{ 16 }+\right.\\ &+& \left. 3 ^2\frac { 1 }{ 16 }+ 3.5 ^2\frac { 2 }{ 16 }+ 4 ^2\frac { 2 }{ 16 }+ 5 ^2\frac { 2 }{ 16 }+ 7 ^2\frac { 1 }{ 16 } \right)-( 2.75 )^2\\ &=& 3.59375 \\ &=& \frac{7.1875}{2}\\ &=& \frac{\sigma^2}{n} \end{eqnarray*}\]
Consideriamo la stima della varianza \[ \hat\sigma^2=\frac 12\left((X_1-\hat\mu)^2+(X_2-\hat\mu)^2\right) \]
\[ \begin{array}{ r|rrrrrrrr } & 0 ;&\color{blue}{ \frac{ 1 } { 4 }} & 1 ;&\color{blue}{ \frac{ 1 } { 4 }} & 3 ;&\color{blue}{ \frac{ 1 } { 4 }} & 7 ;&\color{blue}{ \frac{ 1 } { 4 }} \\ \hline 0 ;\color{blue}{ 1 / 4 }& 0;&\color{red}{\frac{1}{16}}& 0.25;&\color{red}{\frac{1}{16}}& 2.25;&\color{red}{\frac{1}{16}}& 12.25;&\color{red}{\frac{1}{16}}\\ 1 ;\color{blue}{ 1 / 4 }& 0.25;&\color{red}{\frac{1}{16}}& 0;&\color{red}{\frac{1}{16}}& 1;&\color{red}{\frac{1}{16}}& 9;&\color{red}{\frac{1}{16}}\\ 3 ;\color{blue}{ 1 / 4 }& 2.25;&\color{red}{\frac{1}{16}}& 1;&\color{red}{\frac{1}{16}}& 0;&\color{red}{\frac{1}{16}}& 4;&\color{red}{\frac{1}{16}}\\ 7 ;\color{blue}{ 1 / 4 }& 12.25;&\color{red}{\frac{1}{16}}& 9;&\color{red}{\frac{1}{16}}& 4;&\color{red}{\frac{1}{16}}& 0;&\color{red}{\frac{1}{16}}\\ \end{array} \]
E ricaviamo la distribuzione di, \(\hat\sigma^2\)
\[ \begin{array}{ r|rrrrrrr } \hat\sigma^2 & 0& 0.25& 1& 2.25& 4& 9& 12.25 \\ \hline P( \hat\sigma^2 ) & \frac{4}{16}& \frac{2}{16}& \frac{2}{16}& \frac{2}{16}& \frac{2}{16}& \frac{2}{16}& \frac{2}{16} \\ \end{array} \]
e osserviamo che
\[\begin{eqnarray*} E(\hat\sigma^2) &=& \sum_{\hat\sigma^2}\hat\sigma^2 P(\hat\sigma^2)\\ &=& 0 \frac { 4 }{ 16 }+ 0.25 \frac { 2 }{ 16 }+ 1 \frac { 2 }{ 16 }+ 2.25 \frac { 2 }{ 16 }+ \\ &+& 4 \frac { 2 }{ 16 }+ 9 \frac { 2 }{ 16 }+ 12.25 \frac { 2 }{ 16 } \\ &=& 3.59375 \\ &=& \frac{1}{2}7.1875\\ &=& \frac{n-1}{n}\sigma^2 \end{eqnarray*}\]
11.3.7 Distribuzione delle statistiche
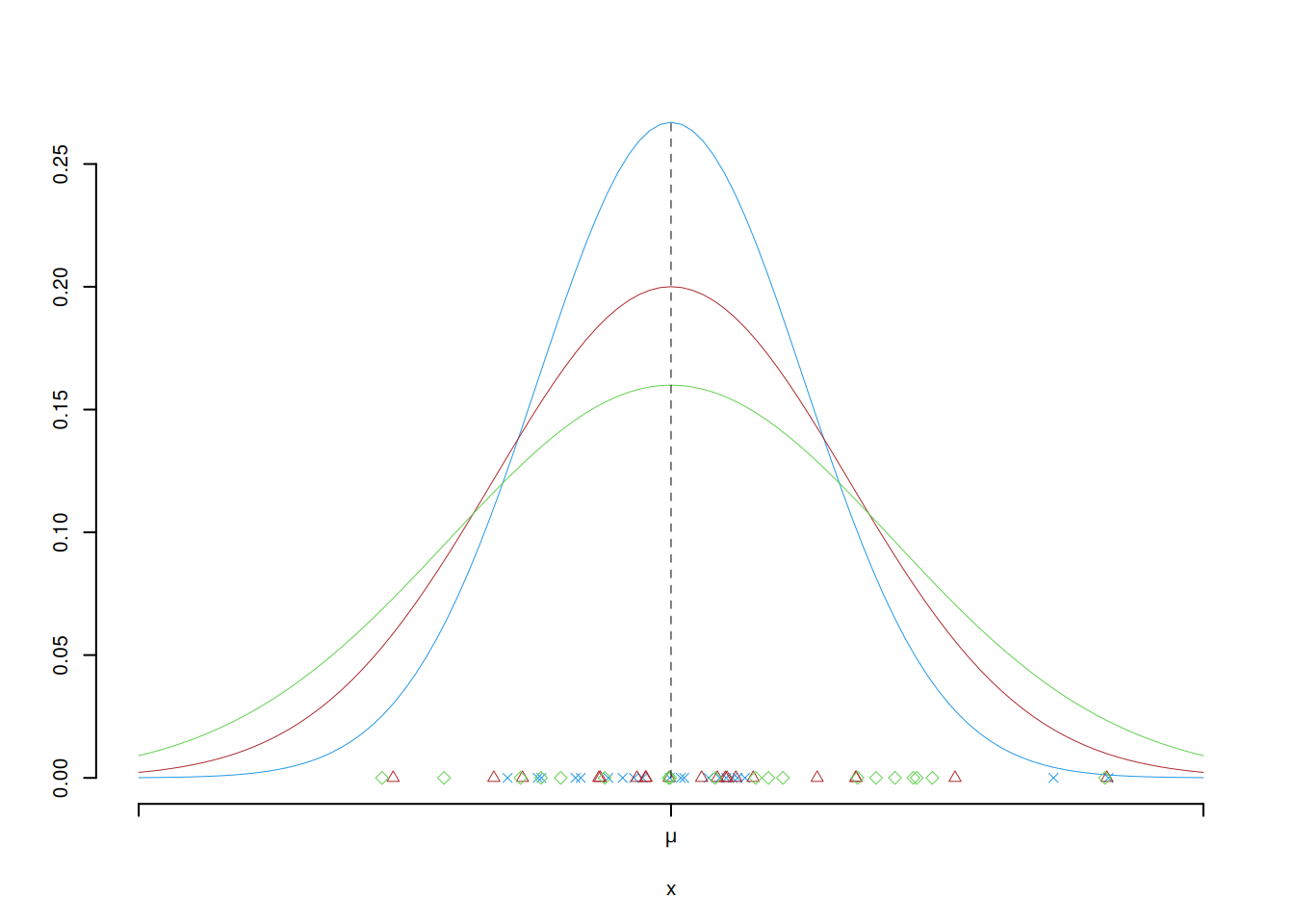
Supponiamo di estrarre campioni di ampiezza \(n\) CR da una popolazione con media \(\mu\) e varianza \(\sigma^2\). Osservo tre diversi stimatori per \(\mu\): \(\hat\mu_1\), \(\hat\mu_2\) e \(\hat\mu_3\)
Se si ripetesse l’estrazione un grande numero di volte potremmo vedere i tre stimatori nel grafico qui di seguito. Lo stimatore in con la distribuzione in blu è il più efficiente dei tre: la probabilità che si avveri lontano dal vero parametro è minore che per gli altri due. Mentre lo stimatore in con la distribuzione in verde è il meno efficiente dei tre: la probabilità che si avveri lontano dal vero parametro è maggiore che per gli altri due.
11.3.8 Proprietà Auspicabili di uno stimatore (per \(n\to\infty\))
Siano \(X_1,...,X_n\), \(n\) VC, IID, replicazioni della stessa \(X\sim\mathscr{L}(\theta)\), sia \(\hat\theta\) uno stimatore per \(\theta\).
Definizione 11.4 (Correttezza Asintotica) Lo stimatore \(\hat\theta\) si dice asintoticamente corretto se \[\lim_{n\to\infty}E(\hat\theta(X_1,...,X_n))=E(\hat\theta)=\theta\]
Esempio 11.6 \[\lim_{n\to\infty}E(\hat\sigma^2)=\lim_{n\to\infty}\frac{n-1}n\sigma^2=\sigma^2\]
Definizione 11.5 (Consistenza) Lo stimatore \(\hat\theta\) si dice consistente (in media quadratica) se e solo se \[\lim_{n\to\infty}MSE(\hat\theta(X_1,...,X_n))=\lim_{n\to\infty}MSE(\hat\theta)=0\]
Essendo \[MSE(\hat\theta)=V(\hat\theta)+B^2(\hat\theta)\] allora \[\lim_{n\to\infty} MSE(\hat\theta)=0, \text{ se e solo se} \lim_{n\to\infty} V(\hat\theta)=0 \text{ e } \lim_{n\to\infty} B^2(\hat\theta)=0\]
Esempio 11.7 (Consistenza) Siano \(X_1,...,X_n\), \(n\) VC, IID, replicazioni della stessa VC \(X\) con \(E(X)=\mu\) e \(V(X)=\sigma^2\) Usiamo \(\hat \mu\) per stimare \(\mu\): \[\hat \mu=\frac 1 n \sum_{i=1}^n X_i=\frac {S_n}n\]
Siccome \(\hat \mu\) è stimatore corretto per \(\mu\): \[E(\hat \mu)=E\left(\frac{X_1+...+X_n}{n}\right)=\frac 1 n(E(X_1)+...+E(X_n))=\frac 1 n (\mu+...+\mu)=\mu\]
Allora \[MSE(\hat \mu)=V(\hat \mu)=\frac {\sigma^2}n\]
Al divergere di \(n\) \[\lim_{n\to \infty}MSE(\hat \mu)=\lim_{n\to\infty}\frac{\sigma^2}n=0\]
Lo stimatore \(\hat \mu\) per \(\mu\) è stimatore corretto e consistente.
11.4 La \(SD\) e lo \(SE\)
La standard deviation (SD) \(\sigma\), rappresenta la dispersione degli individui dalla media, è un indicatore di variabilità della popolazione, per esempio in una popolazione finita di \(N\) individui: \[\sigma=\sqrt{\sigma^2}=\sqrt{\frac 1 N\sum_{i=1}^N(x_i-\mu)^2},\] la deviazione standard \(\sigma\) è la radice della varianza della popolazione \(\sigma^2\).
Lo standard error \(SE(\hat\theta)\) di uno stimatore \(\hat\theta\) per \(\theta\) è un indicatore della variabilità dello stimatore nello spazio dei parametri \[SE(\hat\theta)=\sqrt{V(\hat\theta)}\] Lo standard error \(SE(\hat\theta)\) di uno stimatore \(\hat\theta\) per \(\theta\) è la radice della varianza della VC \(\hat\theta\).
La standard deviation stimata \(\sigma\), rappresenta la dispersione degli individui del campione dalla media del campione, è un indicatore di variabilità del campione: \[\hat\sigma=\sqrt{\hat\sigma^2}=\sqrt{\frac 1 n\sum_{i=1}^n(x_i-\hat\mu)^2}\] La deviazione standard stimata \(\hat\sigma\) è la radice della varianza del campione \(\hat\sigma^2\).
Esempio 11.8 Lo standard error dello stimatore media aritmetica campionaria \(\hat\mu\) per \(\mu\) \[SE(\hat \mu)=\sqrt\frac{\sigma^2} n=\frac\sigma {\sqrt{n}}\]
L’errore che si commette nello stimare una media dipende da due fattori
- la standard deviation \(\sigma\) che indica la variabilità degli individui tra di loro
- \(1/\sqrt n\) che è l’inverso dell’ampiezza del campione
Se \(\sigma\) è incognito viene stimato da (come vedremo nel paragrafo (12.9.4)) \[S=\sqrt{S^2}=\sqrt{\frac{n}{n-1}\hat\sigma^2}\]
Ottenendo \[\widehat{SE(\hat\mu)}=\frac S {\sqrt n}\]