Capitolo 3 Media Aritmetica, Varianza e Standard Deviation
3.1 Media Aritmetica
La media tra due numeri \(x_1\) e \(x_2\) il punto centrale
\[\bar x = \frac{x_1+x_2}{2}\]
Esempio. Posto \(x_1=2\), \(x_2=5\), allora \[\bar x =\frac{2+5}{2}=3.5\]
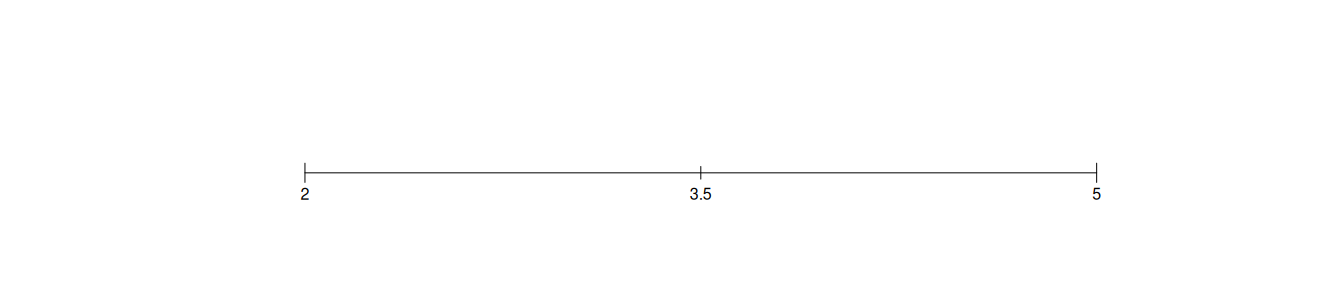
Definizione 3.1 (Media Aritmetica) Consideriamo la serie dei dati \(\mathbf{x}=(x_1,...,x_i,...,x_n)\), si definisce la media aritmetica: \[ \bar x =\frac 1 n \sum_{i=1}^nx_i \]
Ovvero la media tra \(n\) numeri \(x_1, x_2,...,x_n\) è definita da
\[\bar x = \frac{x_1+x_2+...+x_n}{n}\]
siccome la somma dei dati, rappresenta il totale (\(Tot\)) del fenomeno nel collettivo
\[Tot=x_1+x_2+...+x_n=\sum_{i=1}^nx_i \]
allora la media aritmetica
\[\bar x=\frac {Tot}n=\frac 1 n \sum_{i=1}^nx_i \]
rappresenta la quantità ipotetica che ogni individuo possiederebbe se il totale fosse equi-ripartito.
3.1.1 La Media Aritmetica come Baricentro dell’Istogramma
La media aritmetica tiene in equilibrio l’istogramma di densità come se si trattase di un sistema fisico. Se per esempio consideriamo 3 diverse serie di dati \[\begin{eqnarray*} \mathbf{x}_1 &=& (x_1 =1,x_2=2,x_3=2,x_4=3)\\ \mathbf{x}_2 &=& (x_1 =1,x_2=2,x_3=2,x_4=5)\\ \mathbf{x}_3 &=& (x_1 =1,x_2=2,x_3=2,x_4=7) \end{eqnarray*}\]
E osserviamo che
\[\begin{eqnarray*} \bar x_1 &=& \frac{1+2+2+3}{4}=2\\ \bar x_2 &=&\frac{1+2+2+5}{4}=2.5\\ \bar x_3 &=&\frac{1+2+2+7}{4}=3 \end{eqnarray*}\]
Ovvero spostando l’ultimo dato verso valori maggiori spingiamo la media su valori maggiori. Graficamente osserviamo come la medie tenga in equilibrio l’istogramma nella figura 3.1.
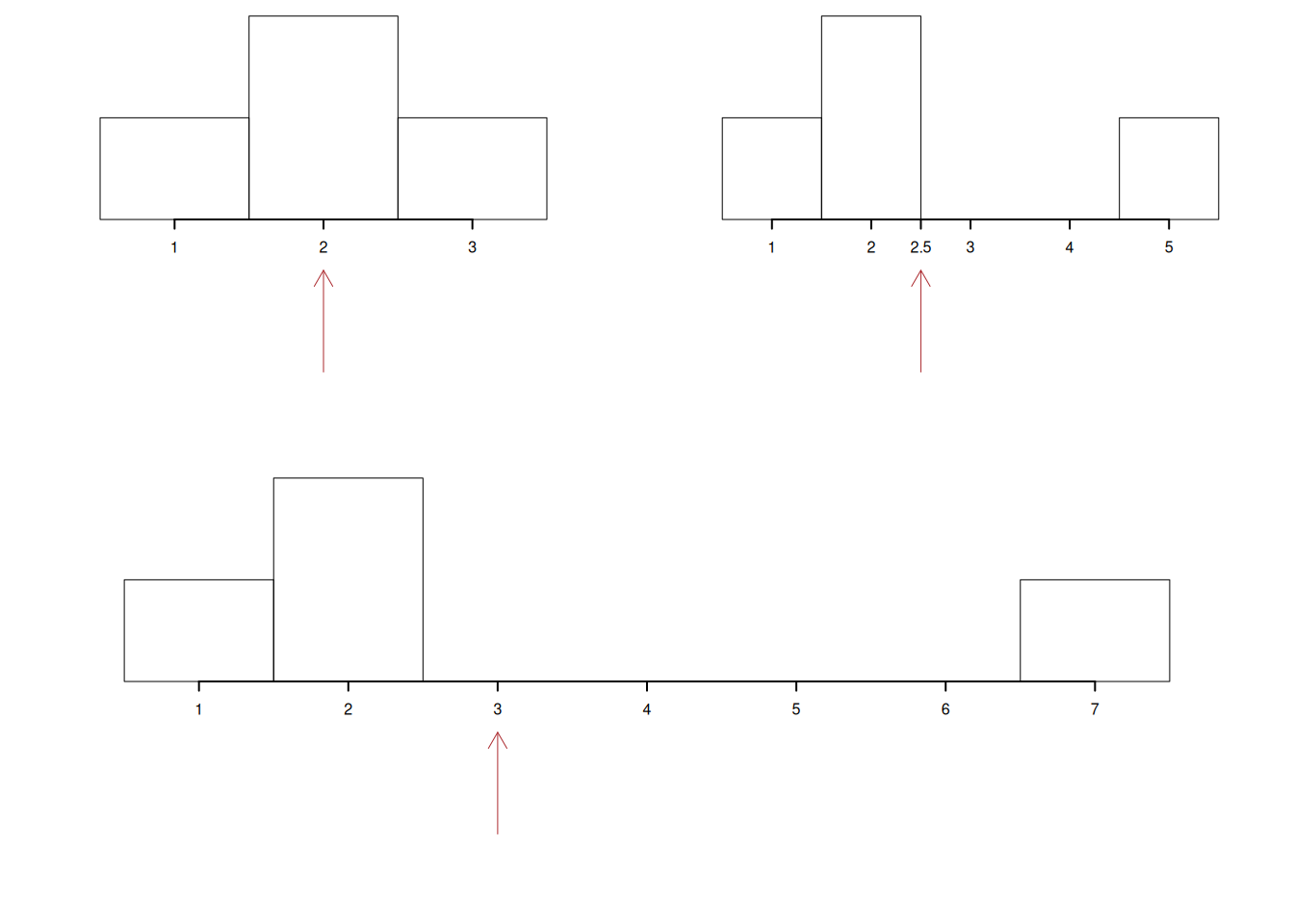
Figura 3.1: La media artimetica tiene in equiibrio l’istogramma di densità, più ci sono dati estremi molto grandi più la media sale per mantenere l’equilibrio col totale.
Allo stesso modo se osserviamo:
\[\begin{eqnarray*} \mathbf{x}_4 &=& (x_1 =-1,x_2=2,x_3=2,x_4=3)\\ \mathbf{x}_5 &=& (x_1 =-3,x_2=2,x_3=2,x_4=3), \end{eqnarray*}\]
allora
\[\begin{eqnarray*} \bar x_1 &=& \frac{1+2+2+3}{4}=2\\ \bar x_4 &=&\frac{-1+2+2+3}{4}=1.5\\ \bar x_5 &=&\frac{-3+2+2+3}{4}=1 \end{eqnarray*}\]
Ovvero spostando il primo dato verso valori minori spingiamo la media su valori minori. Graficamente osserviamo come la media tenga in equilibrio l’istogramma nella figura 3.2.
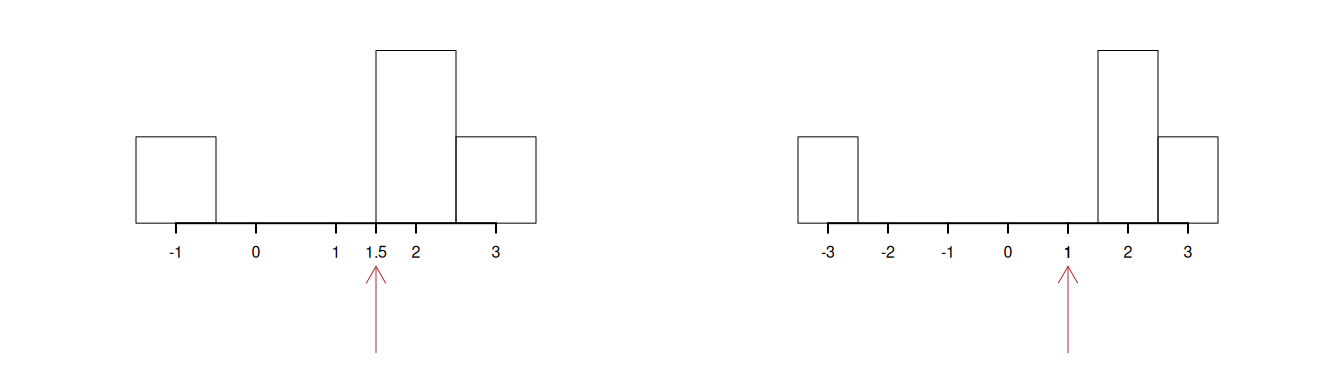
Figura 3.2: Analogamente se spostiamo un dato verso sinistra la media si sposta a sinistra anch’essa
3.1.2 Calcolo per Distribuzioni di Frequenza
Se i dati sono raccolti in distribuzione di frequenza| Modalità | \(\mathrm{x}_1\) | \(\mathrm{x}_2\) | \(\ldots\) | \(\mathrm{x}_j\) | \(\ldots\) | \(\mathrm{x}_K\) | |
| Frequenze | \(n_1\) | \(n_2\) | \(\ldots\) | \(n_j\) | \(\ldots\) | \(n_K\) | \(n\) |
Definizione 3.2 (Media Artimetica per Dati Raccolti in Classi) \[ \bar x =\frac 1 n \sum_{j=1}^K\mathrm{x}_j n_j \]
Esempio 3.1 Osserviamo i seguenti dati: \(x_{1}=3.4\); \(x_{2}=3.4\); \(x_{3}=2.7\); \(x_{4}=3.4\); \(x_{5}=2.7\); \(x_{6}=3.4\); \(x_{7}=2.7\); \(x_{8}=5.1\); \(x_{9}=5.1\); \(x_{10}=2.7\);
La media
\[\begin{eqnarray*} \bar x &=&\frac 1 n \sum_{i=1}^nx_i \\ &=& \frac{x_{1}+x_{2}+x_{3}+x_{4}+x_{5}+x_{6}+x_{7}+x_{8}+x_{9}+x_{10}} {10} \\ &=& \frac{3.4+3.4+2.7+3.4+2.7+3.4+2.7+5.1+5.1+2.7} {10} \\ &=& \frac{34.6} {10}\\ &=& 3.46 \end{eqnarray*}\]
Riordiniamo i dati: \(x_{(1)}=2.7\); \(x_{(2)}=2.7\); \(x_{(3)}=2.7\); \(x_{(4)}=2.7\); \(x_{(5)}=3.4\); \(x_{(6)}=3.4\); \(x_{(7)}=3.4\); \(x_{(8)}=3.4\); \(x_{(9)}=5.1\); \(x_{(10)}=5.1\);
E raccogliamo in distribuzione di frequenza:| modalita | \(\mathrm{x}_1=2.7\) | \(\mathrm{x}_2=3.4\) | \(\mathrm{x}_3=5.1\) | |
| frequenze | 4 | 4 | 2 | 10 |
la media:
\[\begin{eqnarray*} \bar x &=&\frac 1 n \sum_{j=1}^K\mathrm{x}_j n_j \\ &=& \frac{\mathrm{x}_1 n_1+\mathrm{x}_2 n_2+\mathrm{x}_3 n_3} n \\ &=& \frac{2.7\times 4+3.4\times 4+5.1\times 2} {10} \\ &=& \frac{34.6} {10} \\ &=& 3.46 \end{eqnarray*}\]
3.1.3 Proprietà della Media Aritmetica
Proprietà 3.1 (della media aritmetica) Le principale proprietà della media aritmetica sono:
Internalità: \(x_{\min} = x_{(1)} \le \bar{x} \le x_{(n)} = x_{\max}\)
Invarianza della somma: \[n\bar x=\sum_{i=1}^n x_i\]
Somma degli scarti dalla media nulla: \(\sum_{i=1}^{n} (x_{i} - \bar{x}) = 0\)
Minimizza la somma degli scarti al quadrato: \[ \sum_{i=1}^{n} (x_{i} - \bar{x})^{2} < \sum_{i=1}^{n} (x_{i} - d)^{2} \quad \forall d \ne \bar{x} \]
Invarianza per trasformazioni lineari: se \(y_i=a+bx_i\) allora \(\bar{y} = a + b \bar{x}\)
Associatività. Sia una popolazione, \(\mathscr{P}\), formata da \(K\) gruppi con medie e numerosità: (\(\bar{x}_{1};\ n_{1}\)), (\(\bar{x}_{2};\ n_{2}\)), \(\ldots\), (\(\bar{x}_{K};\ n_{K}\)). Allora, la media totale \(\bar{x}_{T}\) di \(\mathscr{P}=\) è data da
\[ \bar{x}_{T} = \frac{\mbox{Tot}{ \{\mathscr{P}}_1\} + \cdots + \mbox{Tot}{ \{\mathscr{P}}_K\}} {n_{1} + \cdots + n_{K}} = \frac{n_{1}\ \bar{x}_{1} + \cdots + n_{K}\ \bar{x}_{K}} {n_{1} + \cdots + n_{K}} \]
Dimostrazione. Qui di seguito le dimostrazioni
La proprietà di internalità deriva dal fatto che la somma dei dati è maggiore della somma di \(n\) volte del più piccolo dei dati \(\sum_{i=1}^n x_i>\sum_{i=1}^n x_{(1)}\). Mentre \(\sum_{i=1}^n x_i<\sum_{i=1}^n x_{(n)}\) la somma dei dati è maggiore della somma di \(n\) volte del più grande dei dati.
La proprietà di invarianza della somma la otteniamo direttamente dalla definizione di media aritmetica. \[\begin{eqnarray*} \bar x &=& \frac 1n\sum_{i=1}^nx_i\\ n\bar x&=&\sum_{i=1}^nx_i. \end{eqnarray*}\]
Somma degli scarti dalla media nulla. Osserviamo che \[\begin{eqnarray*} \sum_{i=1}^n(x_i-\bar x) &=& \sum_{i=1}^n x_i-\sum_{i=1}^n\bar x\\ &=& n\bar x -n\bar x\\ &=&0. \end{eqnarray*}\]
Minimizza la somma degli scarti al quadrato. Se poniamo \(g(x)=\sum_{i=1}^{n} (x_{i} - x)^{2}\) osserviamo che \[\begin{align*} g(x) &= \sum_{i=1}^n(x_i-x)^2 \\ &= (x_1- x)^2+...+(x_n- x)^2 && \text{La funzione $g$ è una somma di parabole}\\ g'(x) &= -2(x_1- x)-...-2(x_n- x) && \text{Dove $g'$ indica la derivata prima di $g$}\\ &= -2\sum_{i=1}^nx_i -2nx\\ g'(x) &= 0 && \text{Eguagliamo $g'$ a zero per avere il minimo}\\ -2\sum_{i=1}^nx_i -2nx&=0\\ x&=\frac 1n\sum_{i=1}^nx_i. \end{align*}\]
Invarianza per trasformazioni lineari: se \(y_i=a+bx_i\) allora
\[\begin{eqnarray*} \bar y &=& \frac 1n\sum_{i=1}^n y_i \\ &=& \frac 1n\sum_{i=1}^n (a+bx_i)\\ &=& \frac 1n\sum_{i=1}^n a + \frac 1n\sum_{i=1}^n bx\\ &=& a+b\bar x. \end{eqnarray*}\]
- Associatività. Sia una popolazione, \(\mathscr{P}\), formata da \(K\) gruppi con medie e numerosità: (\(\bar{x}_{1};\ n_{1}\)), (\(\bar{x}_{2};\ n_{2}\)), \(\ldots\), (\(\bar{x}_{K};\ n_{K}\)). Allora, il totale di tutte le popolazioni è \(Tot=n_1\bar x_1+...+n_1\bar x_K\), mentre il numero totale di individui di tutte e \(K\) le popolazioni è \(n_T=n_1+...+n_K\) E quindi la media
\[ \bar{x}_{T} = \frac{\mbox{Tot}{ \{\mathscr{P}}_1\} + \cdots + \mbox{Tot}{ \{\mathscr{P}}_K\}} {n_{1} + \cdots + n_{K}} = \frac{n_{1}\ \bar{x}_{1} + \cdots + n_{K}\ \bar{x}_{K}} {n_{1} + \cdots + n_{K}} \]
3.2 La varianza
La media riduce un complesso di \(n\) dati in uno solo. A parità di media i dati possono essere molto diversi tra di loro. Per esempio le due serie di dati
\[\begin{eqnarray*} \mathbf{x}_1 &=& (x_1 =2,x_2=2,x_3=2,x_4=2)\\ \mathbf{x}_2 &=& (x_1 =1,x_2=2,x_3=2,x_4=3)\\ \mathbf{x}_3 &=& (x_1 =0,x_2=0,x_3=0,x_4=8) \end{eqnarray*}\]
hanno tutte la stessa media \(\bar x_1=\bar x_2 =\bar x_3= 2\), ma nel primo caso tutti possiedono la media, nel secondo chi poco e chi tanto, nel terzo caso uno possiede il totale e gli altri 3 nulla.
La varianza misura la distanza dei dati dalla media.
Definizione 3.3 (Varianza) Si definisce la varianza la quantità: \[ \sigma^2=\frac 1 n \sum_{1=1}^n(x_i-\bar x)^2 \]
La varianza misura lo scostamento medio quadratico dei dati dalla media aritmetica; ovvero è la media del quadrato degli scarti.
Con un po’ di algebra si dimostra che
Proprietà 3.2 (Formula Calcolatoria della Varianza) \[ \sigma^2=\frac 1 n \sum_{1=1}^n x_i^2 -\bar x^2 \]
Dimostrazione. \[\begin{eqnarray*} \sigma^2 &=& \frac 1 n \sum_{1=1}^n(x_i-\bar x)^2\\ &=& \frac 1n\sum_{1=1}^n(x_i^2+\bar x^2-2\cdot x_i\cdot \bar x)\\ &=& \frac 1n\sum_{1=1}^n x_i^2+\frac 1n\sum_{1=1}^n \bar x^2-\frac 1n\sum_{1=1}^n2\cdot x_i\cdot \bar x\\ &=& \frac 1n\sum_{1=1}^n x_i^2+\frac nn \bar x^2-\frac 2n\bar x \cdot n\cdot \bar x\\ &=& \frac 1 n \sum_{1=1}^n x_i^2 -\bar x^2 \end{eqnarray*}\]
Quindi la varianza si può calcolare o come media del quadrato degli scarti dalla media o come media dei quadrati meno il quadrato della media.
Esempio 3.2 Posto \(x_1=2\), \(x_2=2\), \(x_3=2\), \(x_4=2\) allora \[\bar x =\frac{2+2+2+2}{4}=2\]
\[ \sigma^2=\frac {(2-2)^2+(2-2)^2+(2-2)^2+(2-2)^2}{4}=0 \]
Tutti gli individui hanno la stessa quantità che è pari alla media, non c’è variabilità, la varianza vale zero.
Esempio 3.3 Posto \(x_1=1\), \(x_2=2\), \(x_3=2\), \(x_4=3\) allora \[\bar x =\frac{2+2+2+2}{4}=2\]
\[ \sigma^2=\frac {(1-2)^2+(2-2)^2+(2-2)^2+(3-2)^2}{4}=0.5 \]
Non tutti gli individui hanno la stessa quantità, c’è variabilità, la varianza è diversa da zero.
Esempio 3.4 Posto \(x_1=0\), \(x_2=0\), \(x_3=0\), \(x_4=8\) allora \[\bar x =\frac{0+0+0+8}{4}=2\]
\[ \sigma^2=\frac {(0-2)^2+(0-2)^2+(0-2)^2+(8-2)^2}{4}=12 \]
Tutto il totale è posseduto da un solo individuo, c’è massima variabilità.
3.2.1 Calcolo per Distribuzioni di Frequenza
Se i dati sono raccolti in distribuzione di frequenza
| Modalità | \(\mathrm{x}_1\) | \(\mathrm{x}_2\) | \(\ldots\) | \(\mathrm{x}_j\) | \(\ldots\) | \(\mathrm{x}_K\) | |
| Frequenze | \(n_1\) | \(n_2\) | \(\ldots\) | \(n_j\) | \(\ldots\) | \(n_K\) | \(n\) |
la varianza si può calcolare
Proprietà 3.3 (Varianza per Dati in Distribuzione di Frequenza) \[ \sigma^2=\frac 1 n\sum_{j=1}^k(\mathrm{x}_j-\bar x)^2n_j \]
e di conseguenza, con un po’ di algebra otteniamo:
Proprietà 3.4 (Formula Calcolatoria per la Varianza per Dati in Distribuzione di Frequenza) \[ \sigma^2=\frac 1 n\sum_{j=1}^k\mathrm{x}_j^2n_j-\bar x^2 \]
Esempio 3.5 \(x_{1}=3.4\); \(x_{2}=3.4\); \(x_{3}=2.7\); \(x_{4}=3.4\); \(x_{5}=2.7\); \(x_{6}=3.4\); \(x_{7}=2.7\); \(x_{8}=5.1\); \(x_{9}=5.1\); \(x_{10}=2.7\);
La media
\[\begin{eqnarray*} \bar x &=&\frac 1 n \sum_{i=1}^nx_i \\ &=& \frac{x_{1}+x_{2}+x_{3}+x_{4}+x_{5}+x_{6}+x_{7}+x_{8}+x_{9}+x_{10}} {10} \\ &=& \frac{3.4+3.4+2.7+3.4+2.7+3.4+2.7+5.1+5.1+2.7} {10} \\ &=& \frac{34.6} {10}\\ &=& 3.46 \end{eqnarray*}\]
La varianza
\[\begin{eqnarray*} \sigma^2 &=& \frac 1 n \sum_{1=1}^n(x_i-\bar x)^2\\ &=& \tiny\frac{(x_{1}-\bar x)^2+(x_{2}-\bar x)^2+(x_{3}-\bar x)^2+(x_{4}-\bar x)^2+(x_{5}-\bar x)^2+(x_{6}-\bar x)^2+(x_{7}-\bar x)^2+(x_{8}-\bar x)^2+(x_{9}-\bar x)^2+(x_{10}-\bar x)^2} {10} \\ &=& \tiny\frac{( 3.4 - 3.46 )^2+( 3.4 - 3.46 )^2+( 2.7 - 3.46 )^2+( 3.4 - 3.46 )^2+( 2.7 - 3.46 )^2+( 3.4 - 3.46 )^2+( 2.7 - 3.46 )^2+( 5.1 - 3.46 )^2+( 5.1 - 3.46 )^2+( 2.7 - 3.46 )^2} {10} \\ &=& \small\frac{0.0036+0.0036+0.5776+0.0036+0.5776+0.0036+0.5776+2.6896+2.6896+0.5776} {10} \\ &=& \frac{7.704} {10}\\ &=& 0.7704 \end{eqnarray*}\]
Osserviamo che
\[\begin{eqnarray*} \sigma^2 &=& \frac 1 n\sum_{i=1}^nx_i^2-\bar x^2\\ &=&\frac{1} {10} (x_{1}^2+x_{2}^2+x_{3}^2+x_{4}^2+x_{5}^2+x_{6}^2+x_{7}^2+x_{8}^2+x_{9}^2+x_{10}^2) -\bar x^2 \\ &=& \frac1 {10}(3.4 ^2+3.4 ^2+2.7 ^2+3.4 ^2+2.7 ^2+3.4 ^2+2.7 ^2+5.1 ^2+5.1 ^2+2.7 ^2)-3.46^2\\ &=& \frac1 {10}(11.56+11.56+7.29+11.56+7.29+11.56+7.29+26.01+26.01+7.29)-11.9716\\ &=& 12.742 -11.9716\\ &=& 0.7704 \end{eqnarray*}\]
Riordiniamo i dati: \(x_{(1)}=2.7\); \(x_{(2)}=2.7\); \(x_{(3)}=2.7\); \(x_{(4)}=2.7\); \(x_{(5)}=3.4\); \(x_{(6)}=3.4\); \(x_{(7)}=3.4\); \(x_{(8)}=3.4\); \(x_{(9)}=5.1\); \(x_{(10)}=5.1\);
E raccogliamo in distribuzione di frequenza:| modalita | \(\mathrm{x}_1=2.7\) | \(\mathrm{x}_2=3.4\) | \(\mathrm{x}_3=5.1\) | |
| frequenze | 4 | 4 | 2 | 10 |
la media:
\[\begin{eqnarray*} \bar x &=&\frac 1 n \sum_{j=1}^K\mathrm{x}_j n_j \\ &=& \frac{\mathrm{x}_1 n_1+\mathrm{x}_2 n_2+\mathrm{x}_3 n_3} n \\ &=& \frac{2.7\times 4+3.4\times 4+5.1\times 2} {10} \\ &=& \frac{34.6} {10} \\ &=& 3.46 \end{eqnarray*}\]
la varianza:
\[\begin{eqnarray*} \sigma^2 &=& \frac 1 n\sum_{j=1}^k(\mathrm{x}_j-\bar x)^2n_j\\ &=&\frac 1 {10}\left((\mathrm{x}_1 -\bar x)^2n_1+(\mathrm{x}_2-\bar x)^2 n_2+(\mathrm{x}_3-\bar x)^2 n_3\right) \\ &=& \frac1 {10}\left((2.7-3.46)^2\times 4+(3.4-3.46)^2\times 4+(5.1-3.46)^2\times 2\right) \\ &=& \frac{7.704} {10}\\ &=& 0.7704 \end{eqnarray*}\]
o alternativamente
\[\begin{eqnarray*} \sigma^2 &=& \frac 1 n\sum_{j=1}^k\mathrm{x}_j^2n_j-\bar x^2\\ &=&\frac 1 {10} (\mathrm{x}_1^2n_1+\mathrm{x}_2^2n_2+\mathrm{x}_3^2n_3)-\bar x^2\\ &=& \frac 1 {10} (2.7^2\times4+3.4^2\times4+5.1^2\times2)-3.46^2\\ &=& \frac 1 {10}\times 127.42-11.9716\\ &=& 0.7704 \end{eqnarray*}\]
Esempio 3.6 \(x_{1}=3.61\); \(x_{2}=3.32\); \(x_{3}=3.16\); \(x_{4}=3.74\); \(x_{5}=3.61\); \(x_{6}=3.61\); \(x_{7}=3.61\); \(x_{8}=3.46\); \(x_{9}=3.61\); \(x_{10}=3.61\); \(x_{11}=3.74\); \(x_{12}=3.32\); \(x_{13}=3.74\); \(x_{14}=3.74\); \(x_{15}=3.74\); \(x_{16}=3.46\); \(x_{17}=3.46\); \(x_{18}=3.46\); \(x_{19}=3.87\); \(x_{20}=3.61\); \(x_{21}=3.61\);
La media:
\[\begin{eqnarray*} \bar x &=& \frac 1 n \sum_{i=1}^n x_i \\ &=& \frac 1 {21} 75.09\\ &=& 3.5757 \end{eqnarray*}\]
La varianza
\[\begin{eqnarray*} \sigma^2 &=& \frac 1 n \sum_{i=1}^n x_i^2 - \bar x ^2 \\ &=& \frac 1 {21} 269.0885 - 3.5757^2\\ &=& 9.238 \end{eqnarray*}\]
riordiniamo i dati
\(x_{(1)}=3.16\); \(x_{(2)}=3.32\); \(x_{(3)}=3.32\); \(x_{(4)}=3.46\); \(x_{(5)}=3.46\); \(x_{(6)}=3.46\); \(x_{(7)}=3.46\); \(x_{(8)}=3.61\); \(x_{(9)}=3.61\); \(x_{(10)}=3.61\); \(x_{(11)}=3.61\); \(x_{(12)}=3.61\); \(x_{(13)}=3.61\); \(x_{(14)}=3.61\); \(x_{(15)}=3.61\); \(x_{(16)}=3.74\); \(x_{(17)}=3.74\); \(x_{(18)}=3.74\); \(x_{(19)}=3.74\); \(x_{(20)}=3.74\); \(x_{(21)}=3.87\);
E raccogliamo in distribuzione di frequenza:
| \(\mathrm{x}_j\) | \(\mathrm{x}_1=3.16\) | \(\mathrm{x}_2=3.32\) | \(\mathrm{x}_3=3.46\) | \(\mathrm{x}_4=3.61\) | \(\mathrm{x}_5=3.74\) | \(\mathrm{x}_6=3.87\) | Tot |
| \(n_j\) | 1 | 2 | 4 | 8 | 5 | 1 | 21 |
| \(\mathrm{x}_j n_j\) | 10 | 22 | 48 | 104 | 70 | 15 | 269 |
| \(\mathrm{x}_j^2 n_j\) | 100 | 242 | 576 | 1352 | 980 | 225 | 3475 |
E osserviamo che
\[\begin{eqnarray*} \bar x &=& \frac 1 n \sum_{j=1}^k \mathrm{x}_j n_j \\ &=& \frac 1 {21} 75.09\\ &=& 3.5757 \end{eqnarray*}\]
e che
\[\begin{eqnarray*} \sigma^2 &=& \frac 1 n \sum_{j=1}^n \mathrm{x}_j^2 n_j - \bar x ^2 \\ &=& \frac 1 {21} 269.0885 - 3.5757^2\\ &=& 9.238 \end{eqnarray*}\]
3.2.2 Proprietà della Varianza
Proprietà 3.5 (della varianza $\sigma^{2}$) Le principale proprietà della varianza sono:
- \(\sigma^{2} \ge 0\).
- \(\sigma^{2}=0\), se e solo se \(X\) è costante.
- Se \(y_i=a+bx_i\) allora \(\sigma^{2}_Y = b^{2} \sigma^{2}_X\).
Dimostrazione. Le dimostrazioni qui di seguito.
\(\sigma^{2} \ge 0\) deriva direttamente dalla definizione, essendo \(\sigma^{2}\) la media di scarti al quadrato e quindi di quantità positive, non potrà mai essere negativa.
\(\sigma^{2}=0\) solo se ogni scarto dalla media è zero e questo può avvenire solo se tutti i dati sono uguali alla media, ovvero se i dati sono tutti uguali tra di loro e quindi non variano.
Se \(y_i=a+bx_i\) allora
\[\begin{eqnarray*} \sigma^{2}_Y &=& \frac 1n \sum_{i=1}^n(y_i-\bar y)^2\\ &=& \frac 1n \sum_{i=1}^n(a+bx_i-(a+b\bar x))^2\\ &=& b^2\frac 1n \sum_{i=1}^n(x_i-\bar x)^2\\ &=& b^2\sigma_X^2 \end{eqnarray*}\]
3.3 La Standard Deviation
La varianza non ha un’unità di misura leggibile, è una media di quadrati degli scarti. E quindi anche l’unità di misura è elevata al quadrato
Si definisce la standard deviation (deviazione standard, scarto quadratico medio), la radice della varianza \[ \sigma=\sqrt{\sigma^2} \]
3.3.1 Proprietà della Standard Deviation
Proprietà 3.6 (della deviazione standard $\sigma$) Le principale proprietà della deviazione standard sono:
- \(\sigma\ge 0\).
- \(\sigma=0\), se e solo se \(X\) è costante.
- Se \(y_i=a+bx_i\) allora allora \(\sigma_Y = |b|\sigma_X\)
Se la distribuzione della \(X\) è abbastanza simmetrica e di forma campanulare, allora
\[ \%(\bar x-2\sigma\le X\le \bar x+2\sigma)\approx 95\% \]
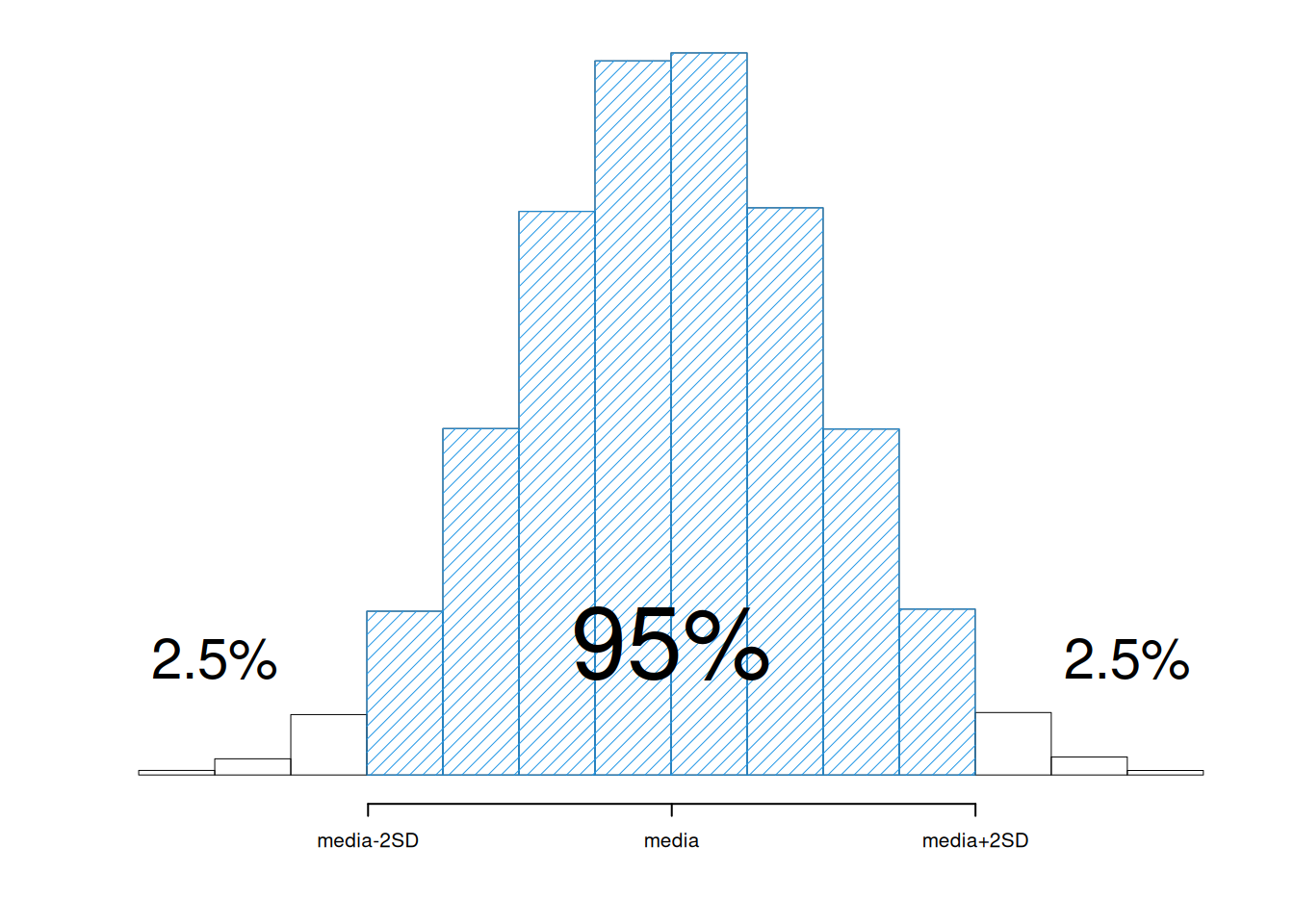
Figura 3.3: Interpretazione della SD
la figura La figura 3.3 la corrispondente rappresentazione grafica.
3.4 Esempi
Esempio 3.7 Si si è chiesta l’età a 37500 uomini e 38100 donne di un determinato collettivo, ed è risultato che gli uomini di quel collettivo hanno un’età media di 45 anni e le donne un’età media di 49 anni. La sintesi dei dati qui di seguito:
| \(n_j\) | \(\bar x_j\) | |
|---|---|---|
| Uomini | 37500 | 45 |
| Donne | 38100 | 49 |
Calcolare l’età media dell’intero collettivo.
Soluzione. L’età media per l’intera popolazione è
Esempio 3.8 Uno studente iscritto al secondo anno di un CdL, ha superato 7 esami con un voto medio pari a 26/30. Sostiene un nuovo esame ottenendo un voto pari a 28/30. Qual è il voto medio dopo l’ottavo esame?
Soluzione. Sia \(\bar{x}_{7}=26\) il voto medio dopo i primi 7 esami. Sia \(\bar{x}_{8}\) il voto medio dopo l’8\(^{o}\) esame. \[\begin{eqnarray*} \bar{x}_{7} &=& \frac{1} {7} \sum_{i=1}^{7} x_{i} \\ \bar{x}_{8} &=& \frac{1} {8} \sum_{i=1}^{8} x_{i} = \frac{1} {8} \left( \sum_{i=1}^{7} x_{i} + x_{8} \right) \\ &=& \frac{1} {8} \left( 7 \bar{x}_{7} + x_{8} \right) = \frac{7 \times \bar{x}_{7} + 1 \times x_{8}} {8} \\ &=& \frac{7 \times 26 + 1 \times 28} {8} = \frac{182 + 28} {8} = 26.25 . \end{eqnarray*}\]
Esempio 3.9 In una contrattazione sindacale, il rappresentante del governo propone di alzare di un ammontare fisso di 100 euro lo stipendio degli impiegati statali.
Come cambierebbero lo stipendio medio e la varianza se questa misura fosse intrapresa?
Se il governo aumentasse lo stipendio di ciascun impiegato statale del 5%, come cambierebbe lo stipendio medio e la varianza?
Soluzione.
- Sia \(x\) lo stipendio degli statali.
\[\begin{eqnarray*} y_{i} &=& x_{i} + 100 \\ \bar{y} &=& \bar{x} + 100 .\\ \sigma_Y^2=\sigma_X^2 \end{eqnarray*}\]
Stipendio medio aumenta esattamente di 100, la varianza non cambia.
- Aumento percentuale pari al 5%.
\[\begin{eqnarray*} y_{i} &=& x_{i} + \frac{5} {100}\ x_{i} = 1.05\ x_{i} \\ \bar{y} &=& 1.05 \bar{x} \\ \sigma_Y^2 &=& (1.05)^2\sigma_X^2 \end{eqnarray*}\]
La MEDIA aumenta del 5%, la varianza aumenta in modo quadratico.
Esempio 3.10 La spesa per le vacanze estive (in migliaia di euro) sostenuta da 12 famiglie di un condominio è stata di:
- Determinare la spesa media e la varianza per famiglia.
\[\begin{eqnarray*} \bar{x} &=& \frac{0 +0 + 2+ 2.5 +4 +5.1 +5.8 +6} {12} + \ldots \\ &+& \frac{7 +12 +15 +21} {12} = \frac{80.4} {12} = 6.7 \mbox{\euro}. \\ \sigma_X^2 &=& \frac{0^2+0^2+2^2+...+21^2}{12}-(6.7)^2\\ &=& 36.8517 \end{eqnarray*}\]
- Determinare la spesa media per famiglie con spesa \(\ne 0\).
\[\begin{eqnarray*} \bar{x} &=& \frac{2+ 2.5 +4 +5.1 +5.8 +6 +7 +12 +15 +21} {10} \\ &=& \frac{80.4} {10} = 8.04 \mbox{\euro}.\\ \sigma_{X}^2 &=& \frac{2^2+...+21^2}{10}-(8.04)^2\\ &=& 33.4484 \end{eqnarray*}\]
Esempio 3.11 Numero di impiegati per anni di servizio di una industria
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(n_j\) | \(f_j\) | \(F_j\) | \(\bar{\text{x}}_j\) | \(\bar{\text{x}}_j^2\) | \(\bar{\text{x}}_jn_j\) | \(\bar{\text{x}}_j^2 n_j\) |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 7 | 0.0609 | 0.0609 | 0.5 | 0.25 | 3.5 | 1.75 |
| 1 | 5 | 18 | 0.1565 | 0.2174 | 3.0 | 9.00 | 54.0 | 162.00 |
| 5 | 10 | 45 | 0.3913 | 0.6087 | 7.5 | 56.25 | 337.5 | 2531.25 |
| 10 | 20 | 25 | 0.2174 | 0.8261 | 15.0 | 225.00 | 375.0 | 5625.00 |
| 20 | 30 | 20 | 0.1739 | 1.0000 | 25.0 | 625.00 | 500.0 | 12500.00 |
| Totale | 115 | 1.0000 | 1270.0 | 20820.00 |
Determinare media, mediana e varianza dell’età di servizio dell’industria.
\[\begin{eqnarray*} \bar{x} &=& \frac{0.5 \times 7 + 3.0 \times 18 + \cdots + 20 \times 25} {7 + 18 + \cdots + 20} = \frac{1270} {115} = 11.04 \\ x_{0.5} &=& x_{m;\ inf} + \frac{0.5 - F_{m-1}} {F_{m} - F_{m-1}} (x_{m;\ sup} - x_{m;\ inf}) \\ &=& 5 + \frac{0.5 - 0.22} {0.61 - 0.22}\ (10 - 5) = 8.59 \\ \sigma_X^2 &=& \frac{1}{115}20820-(11.04)^2\\ &=& 170 \end{eqnarray*}\]