Com’è Realizzato il Libro

Per scrivere queste pagine mi sono avvalso di diverse tecnologie che grazie all’ambiente integrato R-Studio (cita) è possibile combinare insieme con uno sforzo relativamente basso. Tra i tanti software coinvolti ricordo

• R [1]
• R Markdown [2], [3], [4]

R è l’ambiente di calcolo col quale ho svolto tutti i calcoli e realizzato le figure. R Markdown è un software che consente di mescolare pezzi di codici HTML, pezzi di codici \(\rm\LaTeX\) e pezzi di codice R. In sostanza lo stesso documento contiene:

• il contenuto del testo;
• i codici per produrre i calcoli e i grafici;
• i codici che consentono la formattazione del testo

per esempio il codice

```{r, echo=FALSE}
# Questo è un blocco di codice in R
# fisso alcuni parametri ed eseguo alcuni conti
n <- 250 # fisso n = 250
data <- rnorm(n,10,1) # genero n dati da una normale di di media 10 e sd 1
mx <- mean(data) # chiamo mx la media dei dati
vx <- var(data) # chiamo vx la varianza dei dati
```
Abbiamo analizzato $n=`r n`$ individui, abbiamo osservato una media pari 
a $\bar x =`r mx`$ e una varianza pari a $\sigma^2=`r vx`$

```{r, echo=FALSE}
# qui produco un grafico
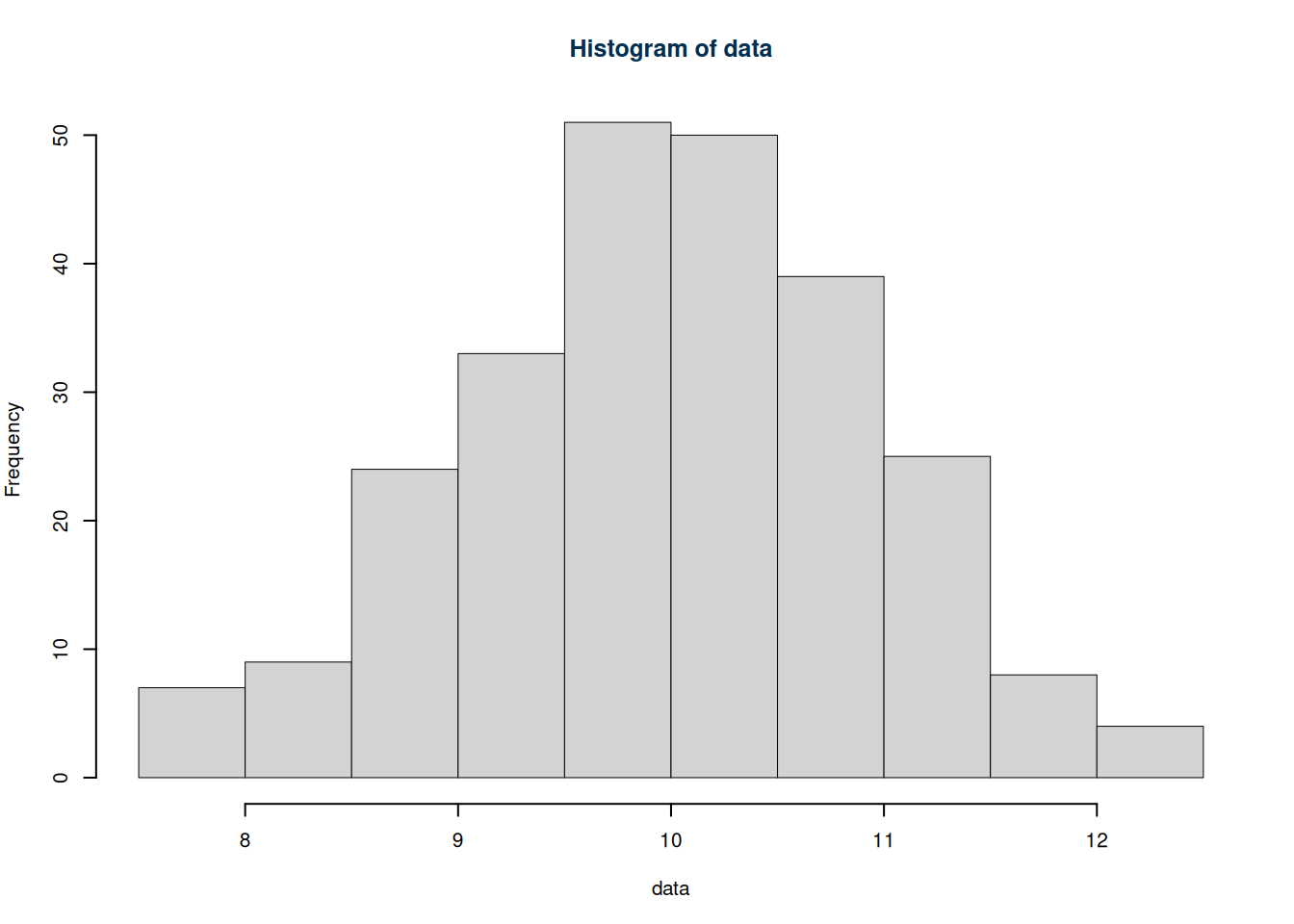
hist(data)
```

produrrà il seguente risultato

Abbiamo analizzato \(n=250\) individui, abbiamo osservato una media pari a \(\bar x =9.982\) e una varianza pari a \(\sigma^2=0.9465\).

Quindi cioè che viene prodotto all’interno dei blocchi di R (chiamati R chunks), è utilizzabile nel testo richiamando `r nome_comando` il testo finale restituirà il risultato di nome_comando.

Le espressioni scritte tra $ sono pezzi di codice che è un potentissimo software di video scrittura, particolarmente adatto per scrivere formule matematiche. Per esempio il codice

$$
\bar x = \frac 1n \sum_{i=1}^n x_i
$$

produce

\[ \bar x = \frac 1n \sum_{i=1}^n x_i \]

L’obiettivo delle seguenti pagine è documentare la realizzazione del libro e non quello di approfondire passo, passo i software utilizzati. Farò solo una breve presentazione per stimolare i lettori più curiosi a cercare documentazioni più approfondite dei principali ambienti che ho utilizzato.

R: A Language and Environment for Statistical Computing

L’ambiente open source R è una collezione software per analizzare, manipolare e rappresentare dati. È sviluppato per tantissimi sistemi operativi tra cui Windows, Linux, Mac OS e tanti altri. Per maggiori informazioni su download e installazione rimando al sito. [https://www.R-project.org/][https://www.R-project.org/] nel quale si trovano diversi documenti di introduzione al software non solo inglese:

• https://cran.r-project.org/manuals.html
• https://cran.r-project.org/other-docs.html

R è un interprete interattivo, l’utente scrive un comando e una volta premuto invio R restituisce il risultato.

R come calcolatrice

R è anzitutto una calcolatrice

1+1 # uno più uno 

## [1] 2

3-4 # tre meno quattro

## [1] -1

4*3 # quattro per tre

## [1] 12

4/3 # 4 diviso 3

## [1] 1.3333

5^2 # cinque elevato alla due

## [1] 25

log(2) # logaritmo naturale di due

## [1] 0.69315

exp(1) # e alla uno, il numero di Nepero

## [1] 2.7183

pi # pi greco, la costante trigonometrica

## [1] 3.1416

1/0 # 1 diviso zero restituisce  infinito

## [1] Inf

Operatori Speciali

Alcuni caratteri speciali sono

• NA Not Available è dedicato ai dati mancanti
• Inf infinito
• NULL non presente, nullo
• TRUE o T vero
• FALSE o F falso

NA+1      # sommare uno al dato mancante dà come risultato un dato mancante

## [1] NA

Inf+1     # infinito più uno è sempre infinito

## [1] Inf

NULL+1    # sommare al nulla uno non restituisce nulla

## numeric(0)

TRUE + 1  # vero + 1 fa due

## [1] 2

FALSE + 1 # falso + 1 fa uno

## [1] 1

• a==b a è uguale a b?
• a!=b a è diverso a b?
• a>b a è maggiore di b?

3 == 4   # 3 è uguale a 4?

## [1] FALSE

3 != 4   # 3 è diverso da 4?

## [1] TRUE

3 >  4   # 3 è maggiore di 4?

## [1] FALSE

Gli operatori & e | svolgono il ruolo di and e or.

cond1 <- TRUE
cond2 <- FALSE

cond1 & cond2 # vera se sono vere entrambe

## [1] FALSE

cond1 | cond2 # vera se almeno una delle due è vera

## [1] TRUE

Vettori e matrici

Con il comando c è possibile concatenare dei valori per creare un vettore, mentre si possono assegnare etichette agli oggetti con l’operatore <-

x <- c(2,1,9)
x

## [1] 2 1 9

y <- c(2.3,1.4,2.8)
y

## [1] 2.3 1.4 2.8

x+y # somma elemento per elemento

## [1]  4.3  2.4 11.8

Alcune funzioni speciali aiutano a velocizzare la creazione di vettori, per esempio 1:10 produce i numeri che vanno da uno a dieci.

1:10

##  [1]  1  2  3  4  5  6  7  8  9 10

Alternativamente la funzione seq produce una sequenza di numeri dal minimo al massimo secondo alcuni criteri

s1 <- seq(0,1,by=.1)     # sequenza da 0 ad 1 di passo 0.1
s2 <- seq(0,1,length=6)  # sequenza da 0 ad 1 di 6 numeri
s1

##  [1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

s2

## [1] 0.0 0.2 0.4 0.6 0.8 1.0

La lunghezza di un vettore si ricava col comando lenght

length(s2)

## [1] 6

Per estrarre elementi da un vettore usiamo le parentesi quadre: s2[2] restituisce il secondo elemento di s2 mentre s2[1:4] restituisce i primi 4 elementi e s2[c(3,2,5)] il terzo, il secondo e il quinto

s2[2]

## [1] 0.2

s2[1:4]

## [1] 0.0 0.2 0.4 0.6

s2[c(3,2,5)]

## [1] 0.4 0.2 0.8

x <- c(1.1,-3.4,4.2,5.1,-4.4,-3.9,2.5)
x > 0 # sequenza di TRUE e FALSE

## [1]  TRUE FALSE  TRUE  TRUE FALSE FALSE  TRUE

which(x > 0) # in quale posizione sono gli x maggiori di zero?

## [1] 1 3 4 7

x[x > 0] # gli x, ma solo quelli maggiori di zero

## [1] 1.1 4.2 5.1 2.5

x[!(x > 0)] # gli x, ma solo quelli che NON sono maggiori di zero

## [1] -3.4 -4.4 -3.9

È possibile costruire matrici con la funzione matrix

mat1 <- matrix(c(1,2,3,4),nrow = 2) # legge in colonna
mat1

##      [,1] [,2]
## [1,]    1    3
## [2,]    2    4

mat2 <- matrix(c(1,2,3,4),nrow = 2,byrow = T) # legge per riga
mat2

##      [,1] [,2]
## [1,]    1    2
## [2,]    3    4

mat1 + mat2 # restituisce la somma elemento per elemento

##      [,1] [,2]
## [1,]    2    5
## [2,]    5    8

Le funzioni cbind ed rdbind consentono di unire una nuova colonna o una nuova riga ad una matrice o vettore.

x1 <- 1:3
x2 <- 2:4
cbind(x1,x2)

##      x1 x2
## [1,]  1  2
## [2,]  2  3
## [3,]  3  4

rbind(x1,x2)

##    [,1] [,2] [,3]
## x1    1    2    3
## x2    2    3    4

Per indicizzare una matrice useremo sempre le parentesi quadre ma con 2 indici

mat <- matrix(1:20,nrow = 5) 
mat

##      [,1] [,2] [,3] [,4]
## [1,]    1    6   11   16
## [2,]    2    7   12   17
## [3,]    3    8   13   18
## [4,]    4    9   14   19
## [5,]    5   10   15   20

mat[1,1]

## [1] 1

mat[2:3,3:4]

##      [,1] [,2]
## [1,]   12   17
## [2,]   13   18

I vettori e le matrici non sono solo numeriche ma possono anche contenere caratteri, ovviamente le operazioni aritmetiche non sono più consentite

mat <- matrix(c("testo 1","testo 2","testo 3","testo 4"),nrow = 2) 
mat

##      [,1]      [,2]     
## [1,] "testo 1" "testo 3"
## [2,] "testo 2" "testo 4"

Liste e dataframe

Una lista è una collezione di diversi oggetti di R

mat1 <- matrix(c(1,2,3,4),nrow = 2) # legge in colonna
mat <- matrix(c("testo 1","testo 2","testo 3","testo 4"),nrow = 2) 
b <- c(NA,NA,NA)

lista <- list(mat1,mat,b)
lista

## [[1]]
##      [,1] [,2]
## [1,]    1    3
## [2,]    2    4
## 
## [[2]]
##      [,1]      [,2]     
## [1,] "testo 1" "testo 3"
## [2,] "testo 2" "testo 4"
## 
## [[3]]
## [1] NA NA NA

Una particolare tipo di lista è il data.frame che consente di creare una matrice dei dati composta da colonne di diversa natura

sesso <- c("M","M","M","F","F")
eta   <- c(32.2,45.6,65.3,34.1,43.2)
dati <- data.frame(sesso,eta)
dati

##   sesso  eta
## 1     M 32.2
## 2     M 45.6
## 3     M 65.3
## 4     F 34.1
## 5     F 43.2

il simbolo del $ aiuta a selezionare le colonne di interesse

dati$sesso

## [1] "M" "M" "M" "F" "F"

dati$eta

## [1] 32.2 45.6 65.3 34.1 43.2

Classi e Oggetti

R è un linguaggio funzionale, ogni elemento è un oggetto che ha un classe e metodi. Per esempio

x <- 3
class(x)

## [1] "numeric"

x <- matrix(1:4,nrow = 2)
class(x)

## [1] "matrix" "array"

x <- list(1:3,c("a","b"))
class(x)

## [1] "list"

Alcuni oggetti possono assomigliarsi ma essere diversi ad esempio

x1 <- 1;3

## [1] 3

x2 <- 2:4
mat <- cbind(x1,x2)
dat <- data.frame(x1,x2)
mat

##      x1 x2
## [1,]  1  2
## [2,]  1  3
## [3,]  1  4

dat

##   x1 x2
## 1  1  2
## 2  1  3
## 3  1  4

class(mat)

## [1] "matrix" "array"

class(dat)

## [1] "data.frame"

I grafici

La libraria grafica di R è particolarmente ricca. La funzione di base per realizzare un grafico è la funzione plot(x,y). La funzione, di default, disegna i punti di coordinate x e y.

x <- c(1,2,3,4)
y <- c(2,1,4,3)
plot(x,y)

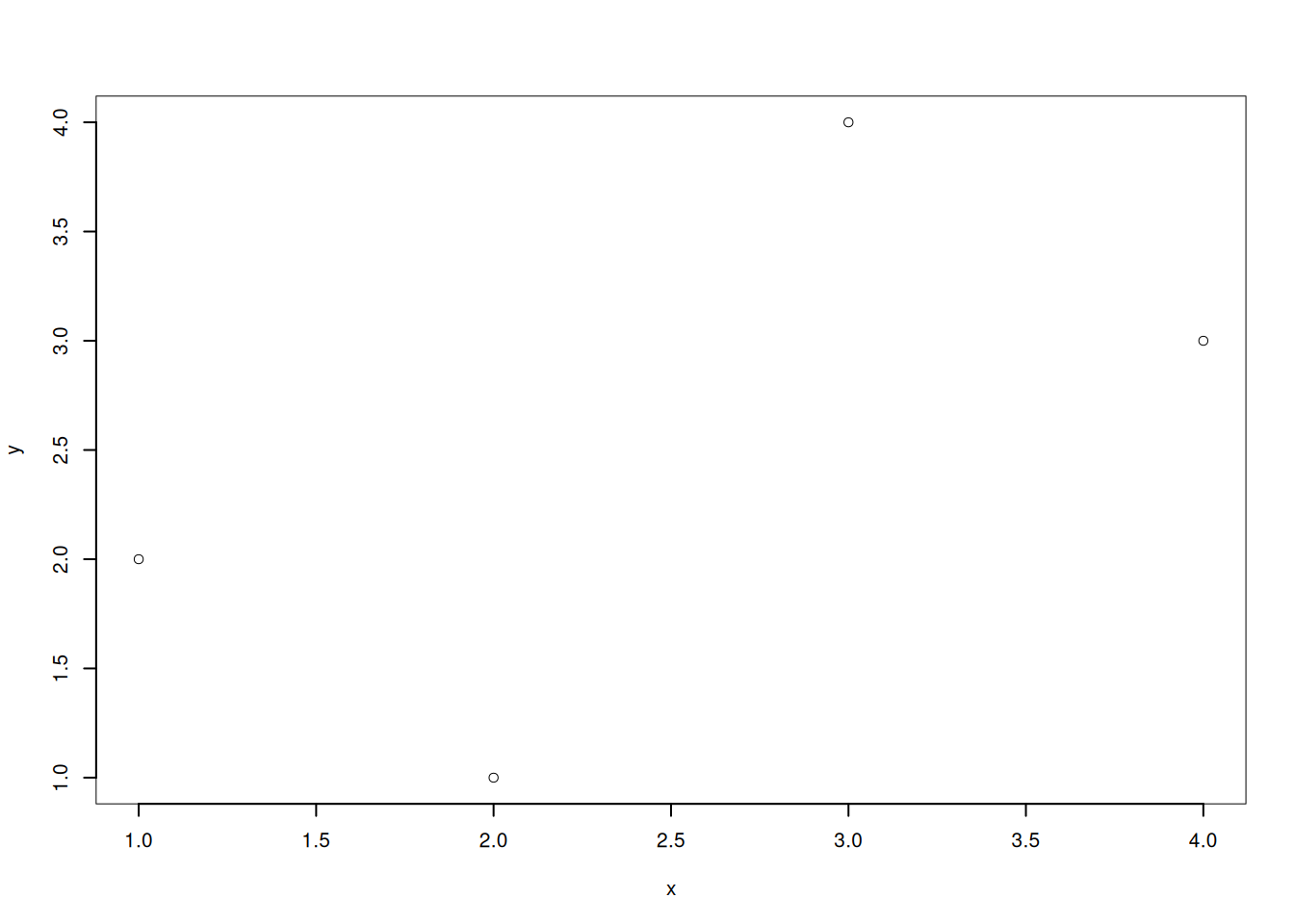
La funzione plot è molto flessibile e può essere arricchita con molte opzioni

x <- c(1,2,3,4)
y <- c(1.9,1.2,3.5,3.1)
plot(x,y,
     axes=F,      # non disegnare gli assi lo farò dopo
     pch = 16,    # codice 16, per il pallino chiuso
     col = ared, #colore rosso per i pallini
     xlab="Etichetta per la x",
     ylab="Etichetta per la y",
     type = "b",  # linea e punto
     lty  =2,     # stile di tratteggiatura
     main = "Titolo del grafico"
          )
# Un volta creato il grafico di base possiamo aggiungere 
axis(1) # asse delle x
axis(2,at = y) # asse delle y sui punti osservati
text(2,3,"Nelle coordinate x=1.5 e y=3 scrivo qualcosa")
text(3,1.9,"Scrivo più grande se cex = 1.5",cex=1.5)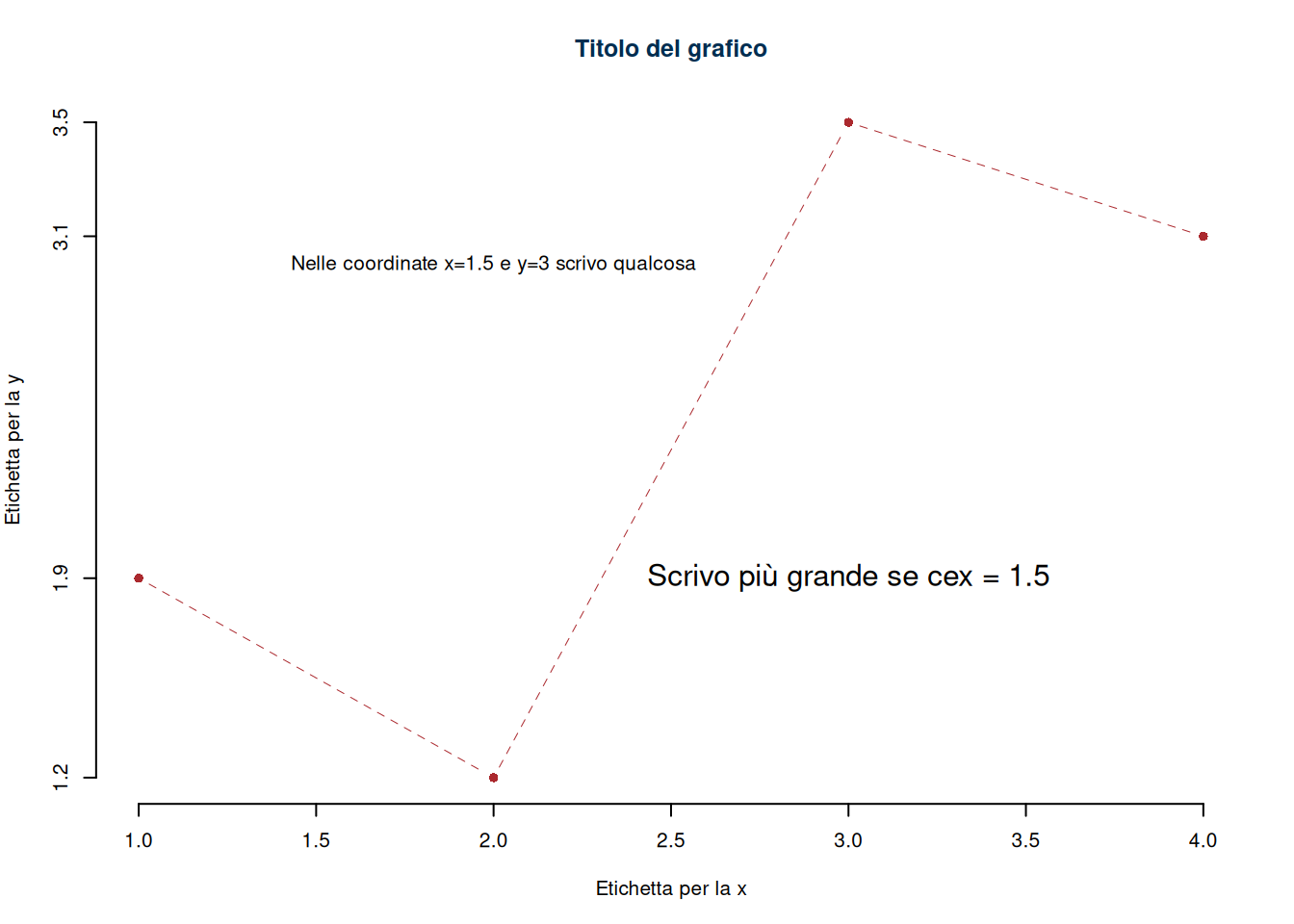

Con le funzioni points e lines è possibile aggiungere al grafico esistente punti e linee, rispettivamente. Mentre per disegnare funzioni la funzione curves aiuta molto

curve(sin(x),from = -pi,to = pi,axes=F) # disegna sin(x) tra - pi e + pi 
curve(cos(x),col=ared,add=T)           # aggiunge il grafico di cos(x) in rosso
points((-3):3,cos((-3):3),pch=3)
lines((-3):3,cos((-3):3),col=iblue,lty=4)
axis(1)
axis(2)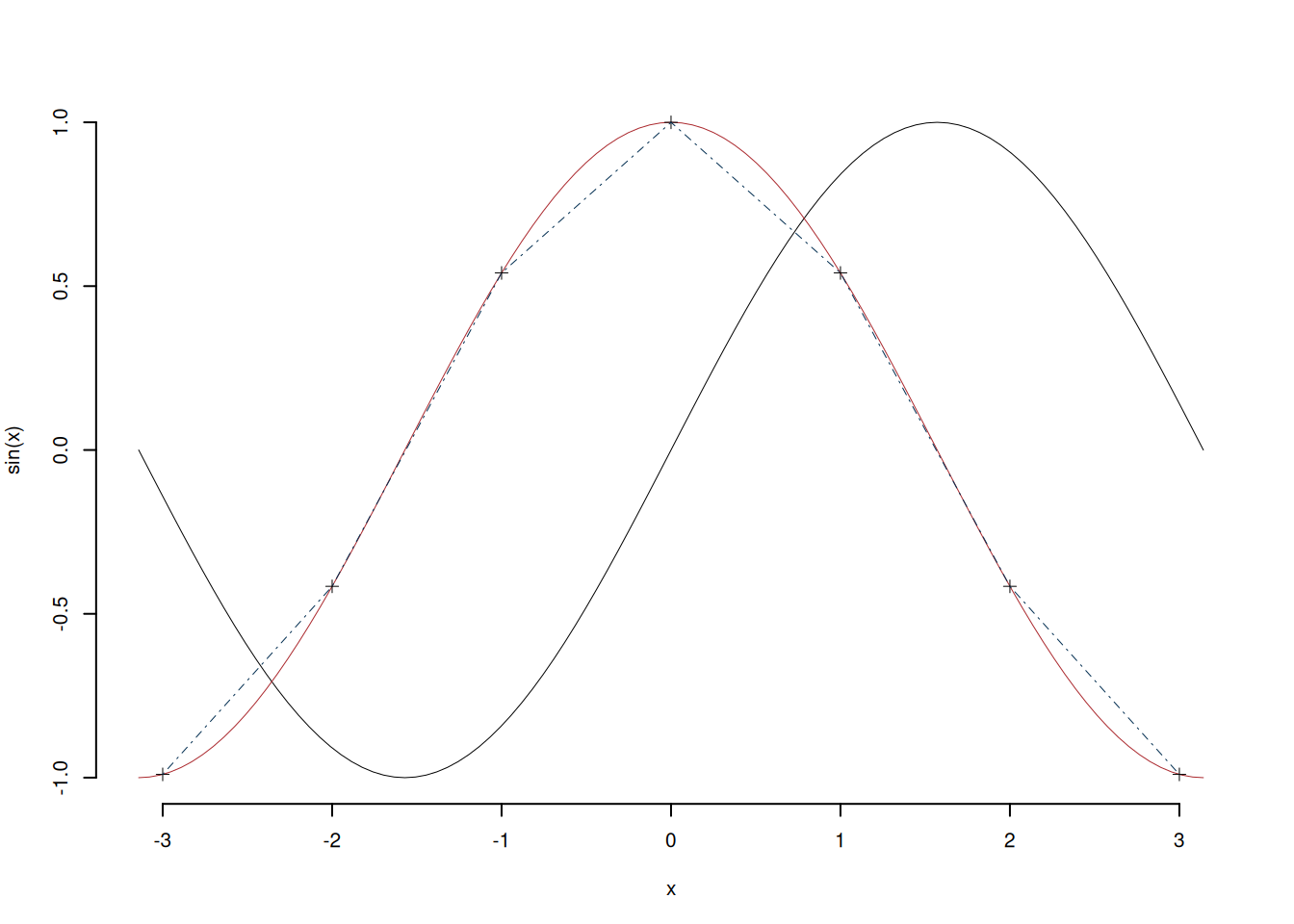

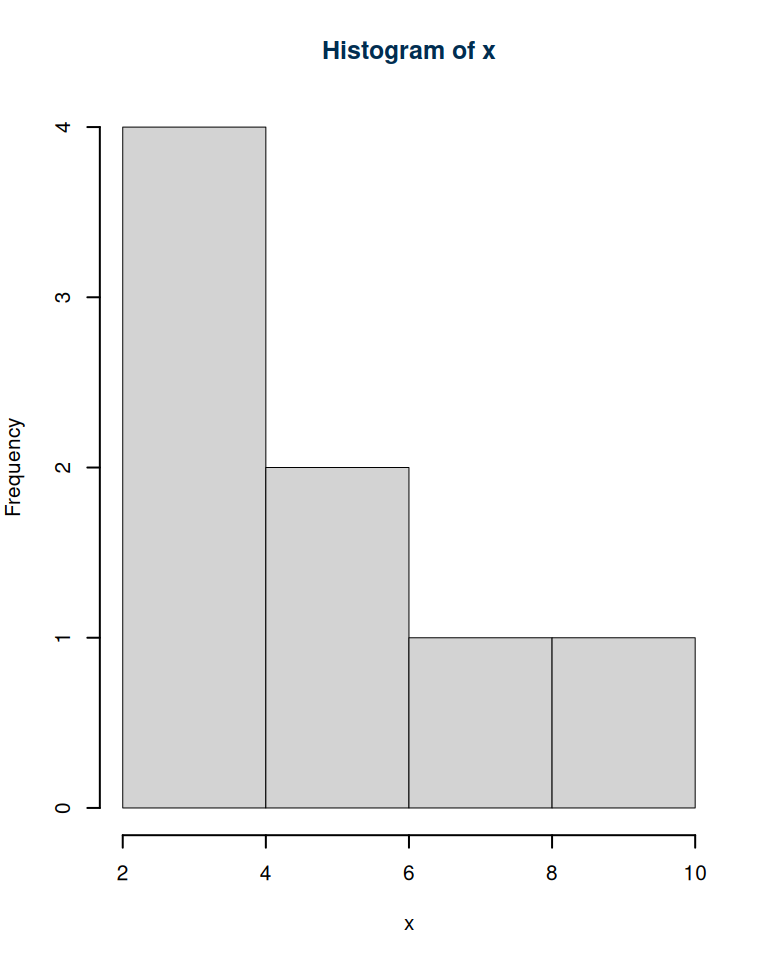
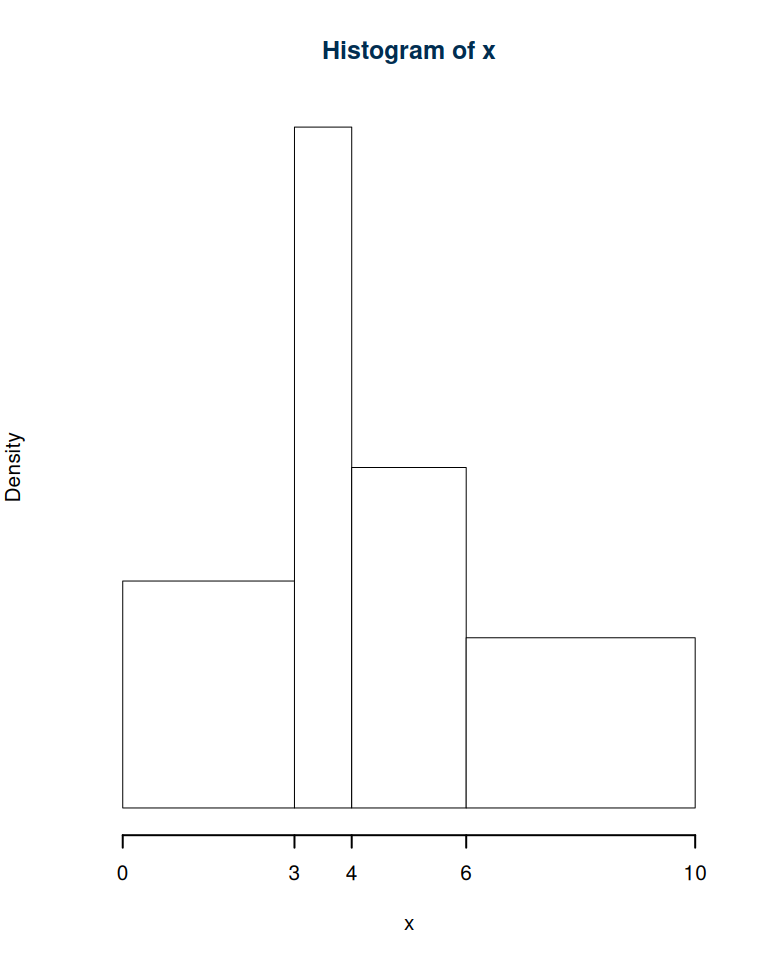
Un’altra funzione di interesse è hist che produce istogrammi di densità

x <- c(2.3,2.5,3.5,3.6,4.6,5.9,6.9,9.8)
hist(x)

hist(x,breaks = c(0,3,4,6,10),probability = T,axes=F,col="white")
axis(1,at = c(0,3,4,6,10))

Per rappresentare dati in 3D la funzione persp disegna superfici in 3 dimensioni

x <- seq(-4,4,by=.1)
y <- seq(-4,4,by=.1)
z <- outer(x,y,function(x,y)exp(-x^2-y^2))
persp(x,y,z,theta = 25,phi = 25,ltheta = 25,border = NA,shade = 2.5)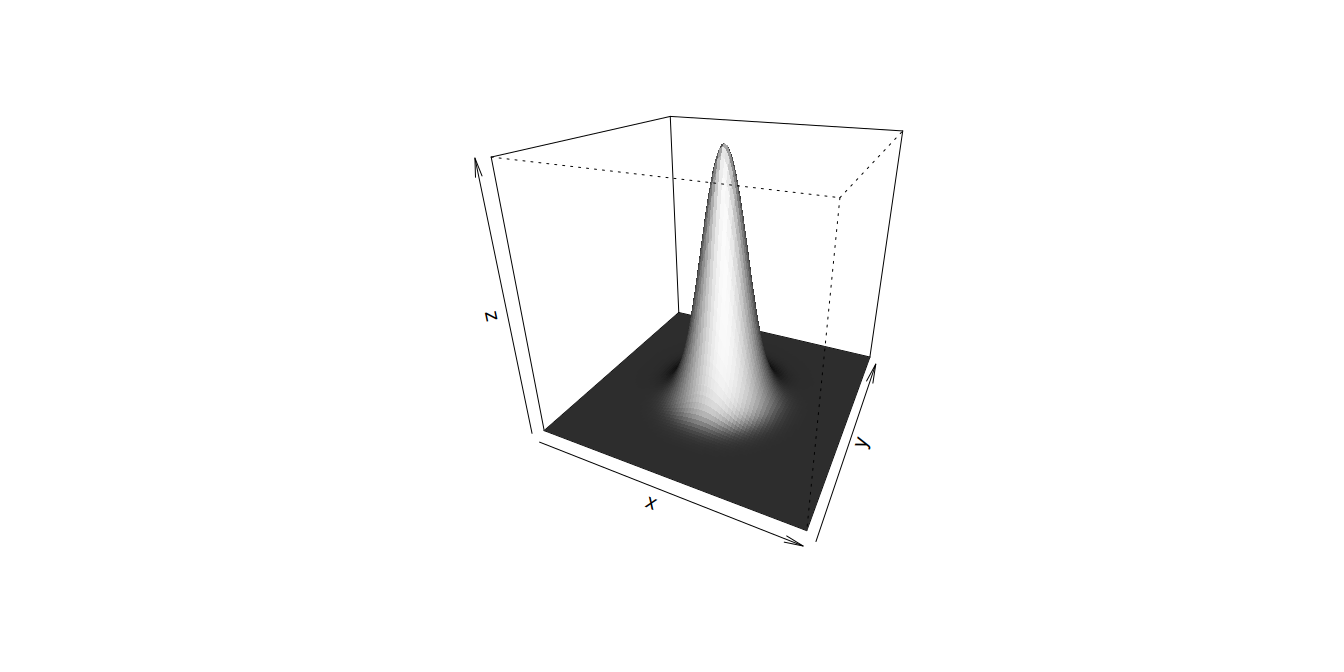

Altre funzioni grafiche interessanti sono rect e polyogn che aggiungo ai grafici rettangoli e poligoni, rispettivamente

plot(c(0,10),c(0,10),xlab = "", ylab="",axes=F,type="n") # inizia un grafico vuoto 
rect(xleft = 1,ybottom = 2,xright = 5,ytop = 4)
rect(xleft = 2,ybottom = 3,xright = 6,ytop = 9,density = 20,col=iblue)
rect(xleft = .5,ybottom = 3.5,xright = 3.5,ytop = 4.5,col=ared)
polygon(x = c(6,6.5,7,10),y = c(1,7,5,6),density = 10,
        col="darkorange",angle = -45,border = "gray39",lwd=4)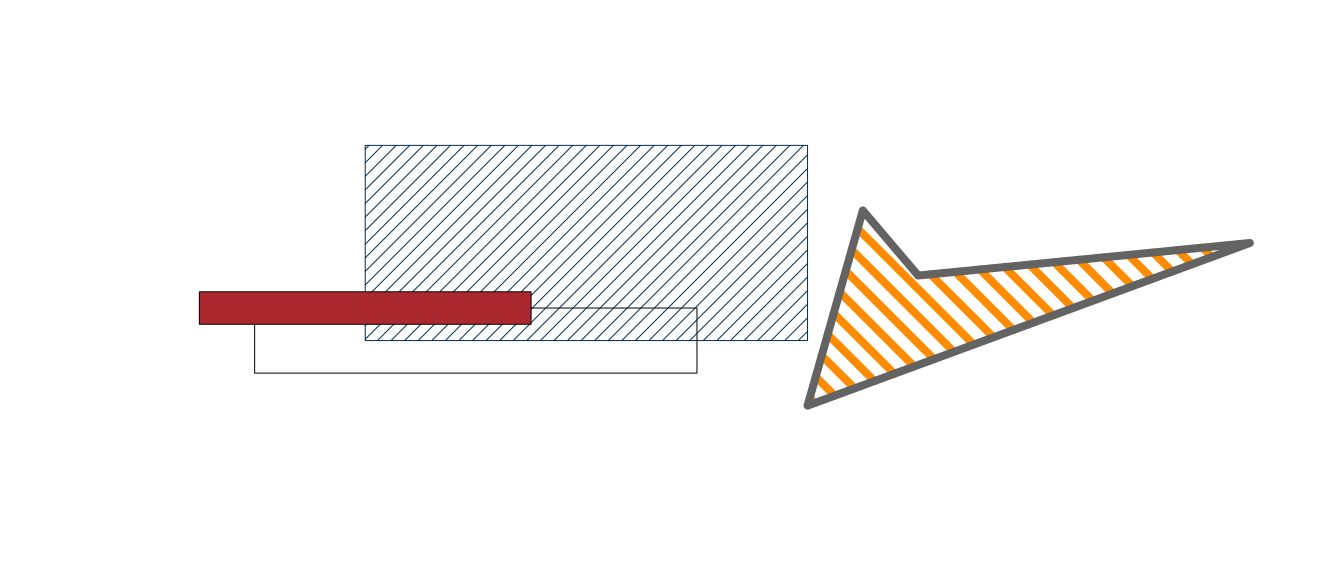

Le proporzioni tra x ed y si possono forzare con l’opzione asp

plot(0:10,0:10,xlab = "", ylab="",axes=F) # asp non specificato
axis(1,pos = 0)
axis(2,pos = 0,las=2)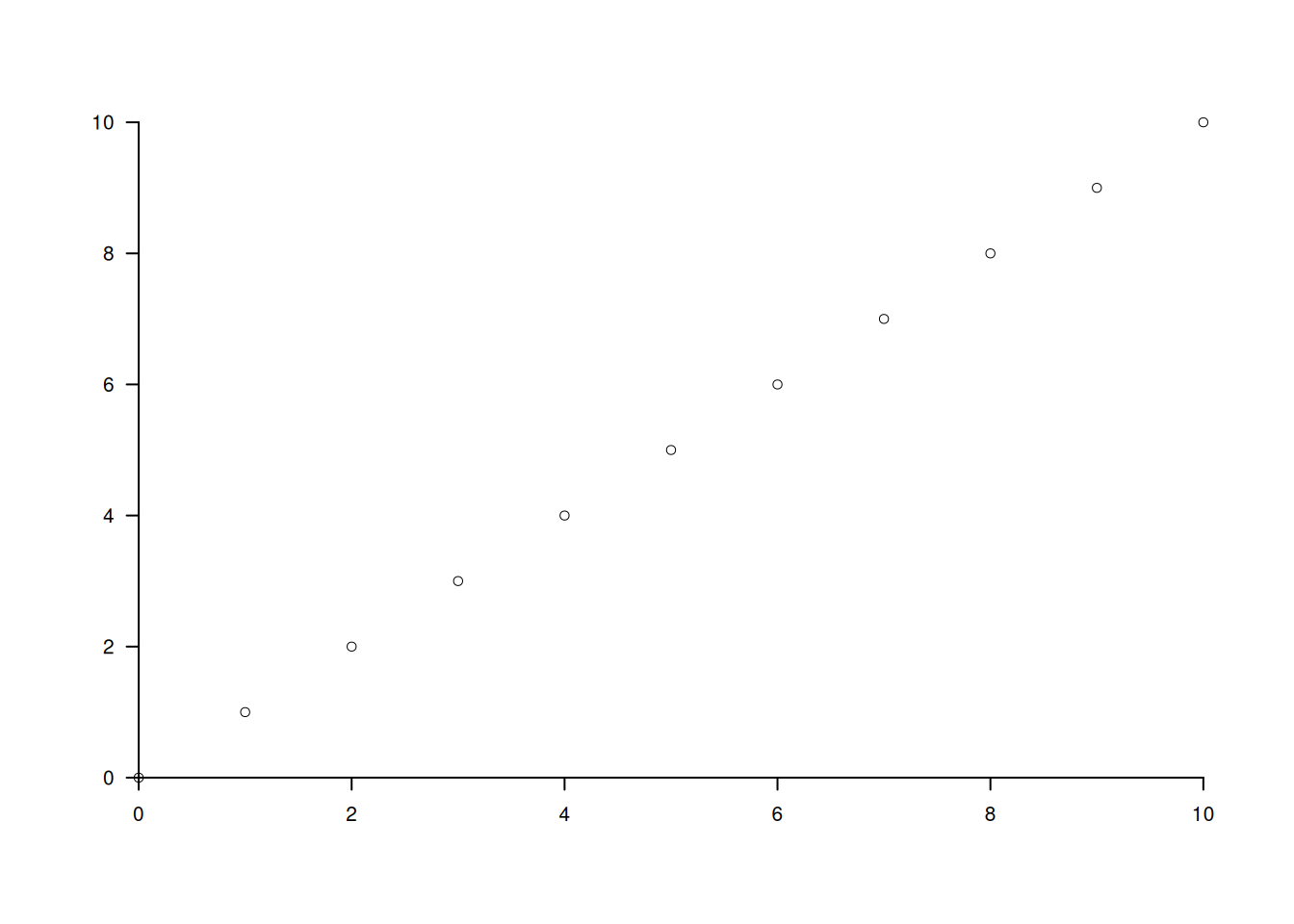

plot(0:10,0:10,xlab = "", ylab="",axes=F,asp=1) # asp=1 
axis(1,pos = 0,at = seq(0,10,by=2))
axis(2,pos = 0,las=2)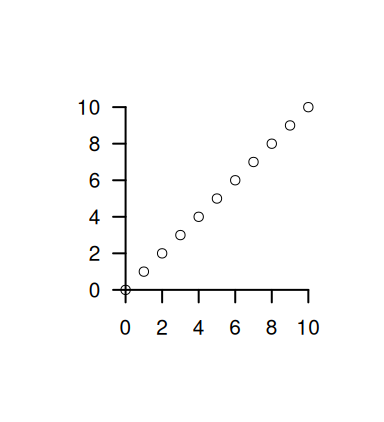

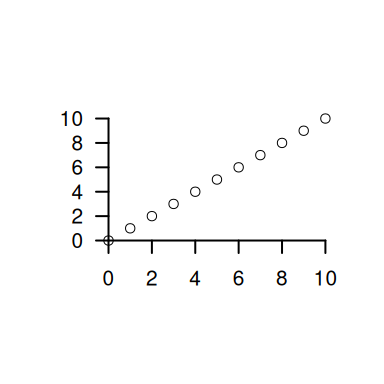
plot(0:10,0:10,xlab = "", ylab="",axes=F,asp=9/16) # asp=9/16 
axis(1,pos = 0)
axis(2,pos = 0,las=2)

plot(0:10,0:10,xlab = "", ylab="",axes=F,asp=4/3) # asp=4/3 
axis(1,pos = 0)
axis(2,pos = 0,las=2,at = seq(0,10,by=2))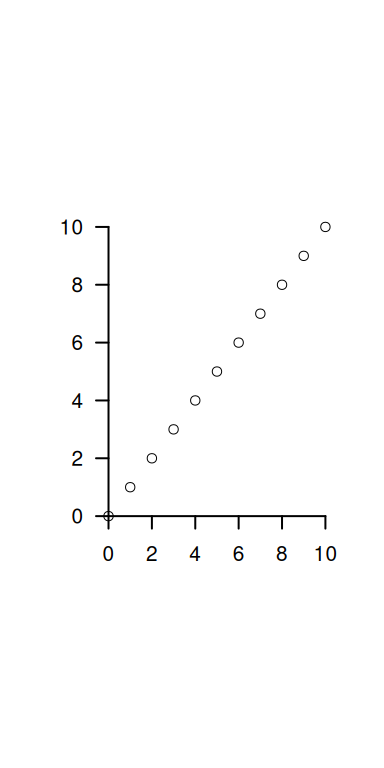

I parametri del grafico si possono settare attraverso par

set.seed(1)
par(mfrow=c(1,2),cex=0.6) # 1 riga e 2 colonne
dati <- rnorm(100) # 100 dati dalla normale
plot(
  sort(dati),(1:100)/100,xlab = "x", ylab="F(x)",axes=F,type="l"
  ) # FdR empirica
axis(1)
axis(2)

hist(
  dati,c(-4,-3,-1.5,-.5,0,.5,1.5,3,4),main="Istogramma di densità",col="white"
  ) # istogramma dei dati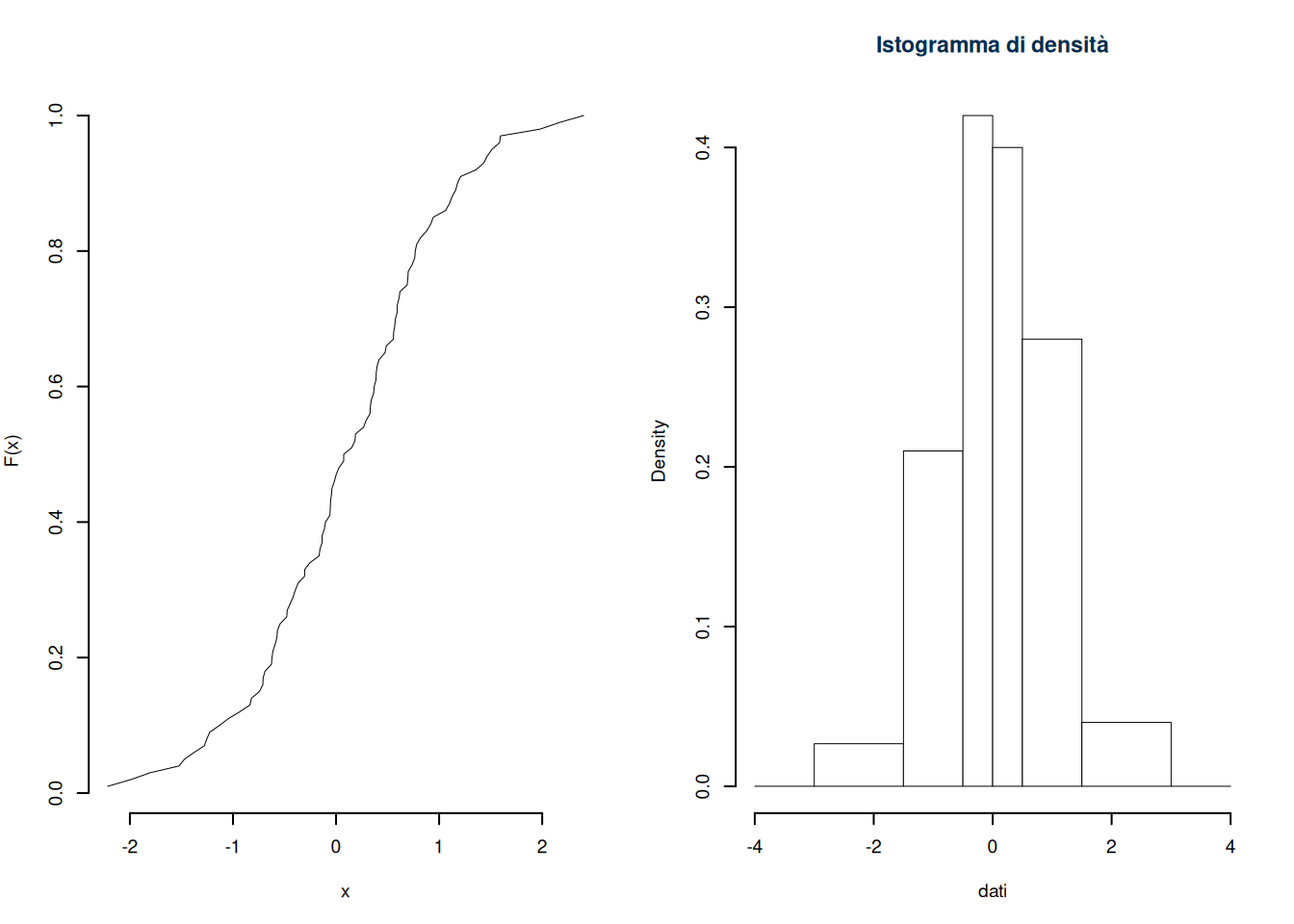

Le Funzioni in R

Essendo R un linguaggio funzionale ogni funzione (che è essa stessa un oggetto) si alimenta di uno o più oggetti di determinate classi e restituisce uno o più oggetti di una determina classe. Per esempio abbiamo visto come la funzione matrix abbia come input un vettore e come output una matrice.

x <- 1:10
class(x)

## [1] "integer"

y <- matrix(x,nrow = 2)
class(y)

## [1] "matrix" "array"

Le funzioni di R hanno argomenti con etichette, se gli argomenti rispettano l’ordine delle etichette non c’è bisogno di chiamarli altrimenti vanno etichettati anche loro. Per esempio la funzione matrix si aspetta almeno due argomenti i dati data e il numero di righe nrow o il numero di colonne ncol

matrix(data,nrow,ncol,byrow = F)

x <- 1:10
matrix(x, 2)                # è identico a

##      [,1] [,2] [,3] [,4] [,5]
## [1,]    1    3    5    7    9
## [2,]    2    4    6    8   10

matrix(nrow = 2, data = x)  # ma è diverso da

##      [,1] [,2] [,3] [,4] [,5]
## [1,]    1    3    5    7    9
## [2,]    2    4    6    8   10

matrix(data = x, ncol = 2)  #

##      [,1] [,2]
## [1,]    1    6
## [2,]    2    7
## [3,]    3    8
## [4,]    4    9
## [5,]    5   10

matrix(2, x)                # produce un risultato senza senso

##      [,1]
## [1,]    2

Le funzioni statistiche

Tra le funzioni di base ricordiamo mean(x) la media del vettore x var(x) la varianza corretta, sd(x) la SD corretta , median(x) la mediana e quantile(x,p) il percentile di ordine \(p\). Per esempio

x <- c(2.3,4.5,6.7,2.1,3.8,2.5,6.9,9.8)
mean(x)   # media

## [1] 4.825

var(x)    # varianza corretta

## [1] 7.5621

sd(x)     # sd corretta

## [1] 2.7499

quantile(x,c(.25,.50,.75)) # i percentili per p=.25,.50,.75 => i quartili

##  25%  50%  75% 
## 2.45 4.15 6.75

Per trattare le variabili doppie nella regressione ci sono strumenti appositi, le funzioni cov(x,y) e cor(x,y) calcolano la correlazione e la covarianza tra i vettori x ed y

x <- c(2.3,4.5,6.7,2.1,3.8,2.5,6.9,9.8)
y <- c(2.4,2.1,5.6,7.2,6.5,7.1,4.3,9.7)
cov(x,y)   # covarianza

## [1] 2.5925

cor(x,y)   # r

## [1] 0.36535

cor(x,y)^2 # r quadro

## [1] 0.13348

La funzione lsfit (Least Squared Fit => Stima dei Minimi Quadrati) consente di calcolare \(\hat\beta_0\) e \(\hat\beta_1\) rapidamente

x <- c(1,2,3,4)
y <- c(1.9,1.2,3.5,3.1)
modello <- lsfit(x,y)
modello$coefficients # coefficienti beta 0 e beta 1

## Intercept         X 
##      0.95      0.59

modello$residuals    # i residui osservati gli epsilon i

## [1]  0.36 -0.93  0.78 -0.21

plot(x,y,
     axes=F,      # non disegnare gli assi lo farò dopo
     pch = 16,    # codice 16, per il pallino chiuso
     col = ared, #colore rosso per i pallini
     xlab="Reddito",
     ylab="Consumo",
     lty  =2,     # stile di tratteggiatura
     main = "Relazione tra Reddito e Conumo"
          )
# Un volta creato il grafico di base possiamo aggiungere 
axis(1) # asse delle x
axis(2) # asse delle y 

# e aggiungere una retta di coefficienti beta 0 e beta 1 

abline(modello$coefficients,lwd=2,col=iblue)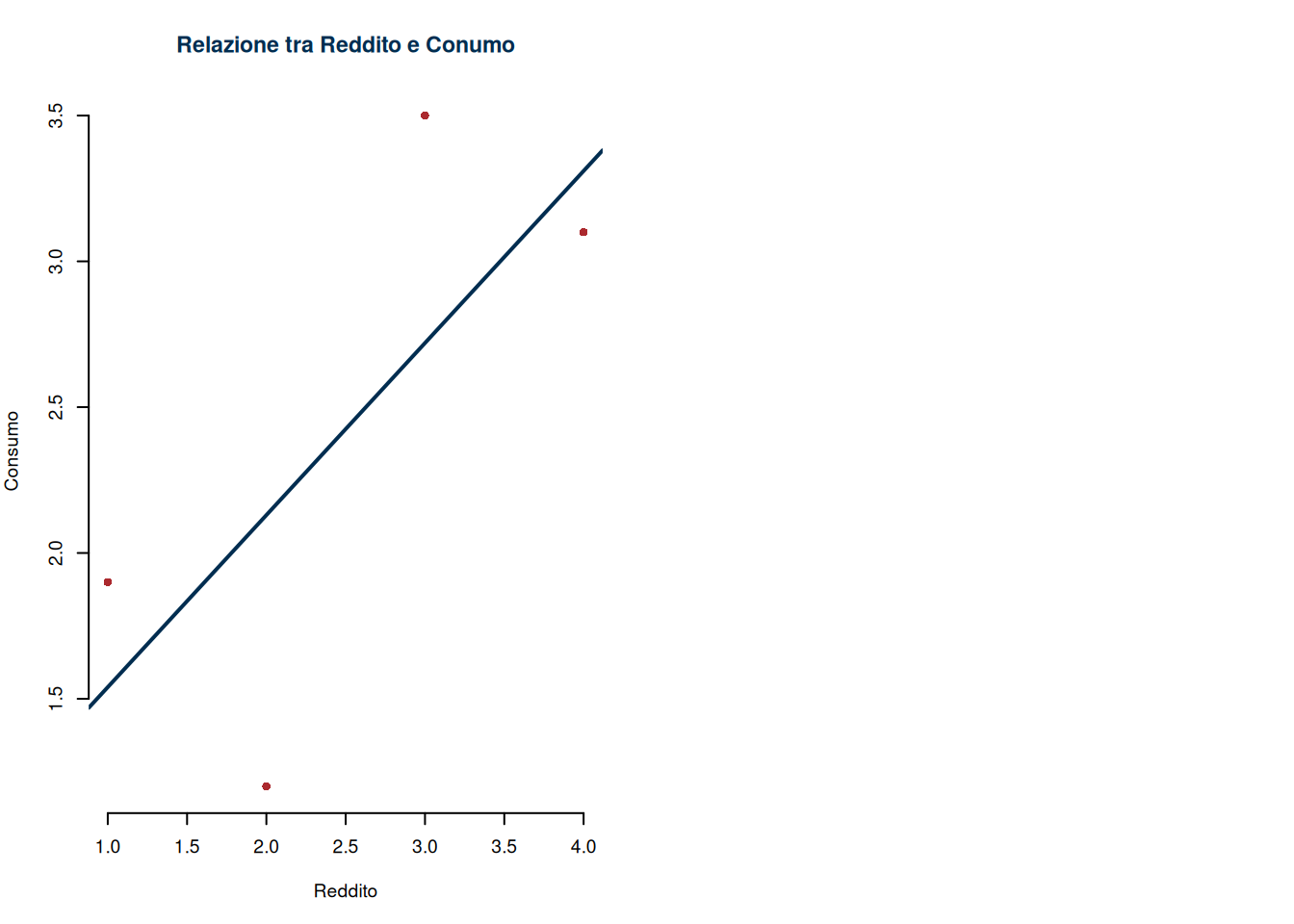 

Le VC di maggiore interessa

In R sono tabulate tutte le distribuzioni di maggiore interesse, comprese, la binomiale, la Poisson, la Normale, la t di studente e il chi quadro, insieme a moltissime altre. La sintassi è relativamente semplice il prefisso d indica la funzione di densità o di probabilità il prefisso p indica la funzione di ripartizione, il prefisso q indica l’inverso della funzione di ripartizione e il prefisso r genera numeri casuali da quella distribuzione. Per esempio se \(X\sim\text{Binom}(n=5;\pi=0.3)\)

dbinom(x = 3,size = 5,prob = 0.3) # è la probabilità che X=3

[1] 0.1323

dbinom(x = 0:5,size = 5,prob = 0.3) #  tutte le probabilità per X=0, 1, ..., 5

[1] 0.16807 0.36015 0.30870 0.13230 0.02835 0.00243

plot(0:5,dbinom(x = 0:5,size = 5,prob = 0.3),type="h",lwd=2) # grafico
pbinom(q = 3,size = 5,prob = 0.3) # è la probabilità che X≤3

[1] 0.96922

qbinom(p = 0.75,size = 5,prob = 0.3) # 75-esimo percentile di X

[1] 2

rbinom(n = 10,size = 5,prob = 0.3)  # simula 10 estrazioni da X

[1] 1 1 1 1 1 1 2 0 1 2

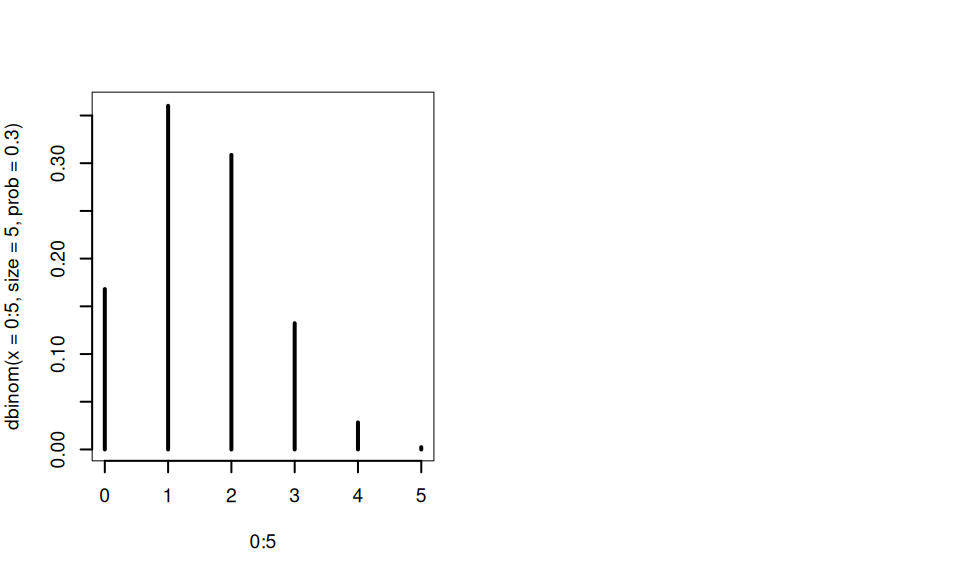
Per esempio se \(X\sim\text{Pois}(\lambda=4.3)\)

dpois(x = 3,lambda = 4.3) # è la probabilità che X=3

[1] 0.1798

dpois(x = 0:10,lambda = 4.3) #  le probabilità per X=0, 1, ..., 10

[1] 0.0135686 0.0583448 0.1254413 0.1797992 0.1932842 0.1662244 0.1191275 [8] 0.0731783 0.0393333 0.0187926 0.0080808

plot(0:10,dpois(x = 0:10,lambda = 4.3),type="h",lwd=2) # grafico
ppois(q = 3,lambda = 4.3) # è la probabilità che X≤3

[1] 0.37715

qpois(p = .75,lambda = 4.3) # 75-esimo percentile di X

[1] 6

rpois(n = 10,lambda = 4.3)  # simula 10 estrazioni da X

[1] 8 2 6 8 6 3 5 8 8 3

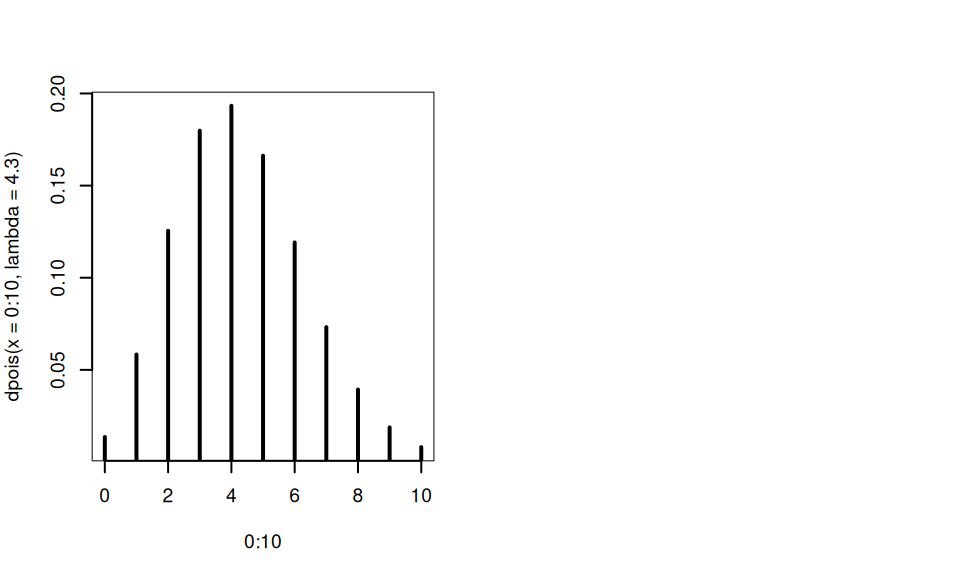
Per esempio se \(X\sim N(\mu=2.5,\sigma^2=(1.5)^2)\)

par(mfrow=c(1,2),cex=0.6) # metto una figura accanto all'altra
curve(dnorm(x,mean = 2.5,sd = 1.5),
      from = 2.5-4*1.5,
      to = 2.5+4*1.5,
      axes=F,
      ylab = expression(f(theta)),
      xlab = expression(theta))
axis(1,c(2.5-2*1.5,2.5-1.5,2.5,2.5+1.5,2.5+2*1.5))
segments(x0 = c(2.5-1.5,2.5+1.5),
         y0 = 0,
         x1 = c(2.5-1.5,2.5+1.5),
         y1 = dnorm(c(2.5-1.5,2.5+1.5),2.5,1.5),
         lty = 2)
curve(pnorm(x,mean = 2.5,sd = 1.5),
      from = 2.5-4*1.5,
      to = 2.5+4*1.5,
      axes=F,
      ylab = expression(F(theta)),
      xlab = expression(theta))
axis(1)
axis(2)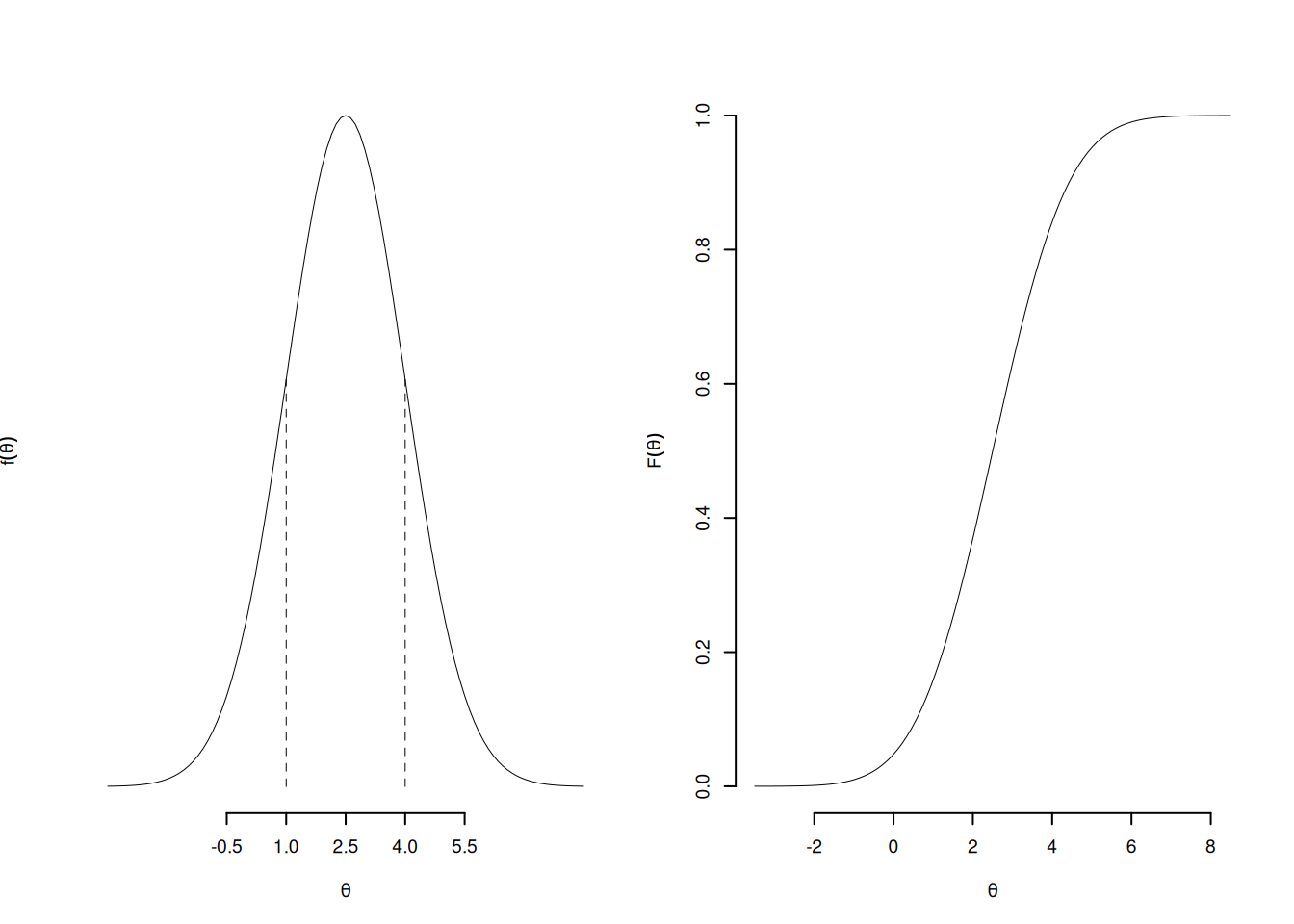

pnorm(3,mean = 2.5,sd = 1.5)      # P(X<3)

## [1] 0.63056

1 - pnorm(3,mean = 2.5,sd = 1.5)  # P(X>3)

## [1] 0.36944

pnorm(3,mean = 2.5,sd = 1.5)-pnorm(0.5,mean = 2.5,sd = 1.5) #  P(0.5 < X < 3)

## [1] 0.53935

rnorm(25,2.5,1.5) # 25 estrazioni da X

##  [1] 1.54640 1.80753 4.64842 1.52396 2.18893 1.91079 2.02001 2.08133 3.24128
## [10] 2.23400 1.74106 4.51456 2.17813 2.23067 2.34971 3.56900 2.38965 2.44355
## [19] 1.47751 2.01359 2.59024 1.61666 3.29724 0.22241 2.95984

Funzioni tra stringhe

Una stringa è un vettore di testo, non numerico, la funzione paste consente di incollare testi.

vettore_testo1 <- c("mela","pera","pesca","banana")
vettore_testo2 <- c("rossa","verde","gialla","gialla")
paste(vettore_testo1,vettore_testo2,sep=" è ")

## [1] "mela è rossa"    "pera è verde"    "pesca è gialla"  "banana è gialla"

paste("la",paste(vettore_testo1,vettore_testo2,sep=" è "),collapse = " e ")

## [1] "la mela è rossa e la pera è verde e la pesca è gialla e la banana è gialla"

x <- round(rnorm(5,10,1),2)
x

## [1] 8.46 9.70 9.47 9.35 9.94

paste("La somma degli x è",paste(x,collapse = " + ")," = ", sum(x))

## [1] "La somma degli x è 8.46 + 9.7 + 9.47 + 9.35 + 9.94  =  46.92"

La funzione cat stampa su schermo o su file e consente l’utilizzo di alcuni caratteri speciali

cat(vettore_testo1,vettore_testo2)

## mela pera pesca banana rossa verde gialla gialla

cat(vettore_testo1,"\t",vettore_testo2)

## mela pera pesca banana    rossa verde gialla gialla

cat(vettore_testo1,"\n",vettore_testo2)

## mela pera pesca banana 
##  rossa verde gialla gialla

Cicli e Condizioni

I cicli si possono fare con for ma come vedremo si possono aggirare in molti modi

for (i in 1:5){
  cat(i,"; ")
}

## 1 ; 2 ; 3 ; 4 ; 5 ;

Mentre le condizioni si risolvono con if else

a <- 12
if (a>10) {
  cat("Hai vinto! \n")
} else {cat("Hai perso! \n")}

## Hai vinto!

a <- 5
if (a>10) {
  cat("Hai vinto! \n")
} else {cat("Hai perso! \n")}

## Hai perso!

anche la funzione ifelse è di aiuto

cond <- TRUE
ifelse(cond,"VERO","FALSO")

## [1] "VERO"

cond <- FALSE
ifelse(cond,"VERO","FALSO")

## [1] "FALSO"

Funzioni per Ovviare ai Cicli

R è un interprete e i cicli rallentano molto il funzionamento dei programmi alcune funzioni speciali quali apply, tapply, lapplay e sapply applicano a diversi tipi di oggetti una funzione. apply applica una funzione alle righe o alle colonne di una matrice

mat <- matrix(rnorm(12),nrow = 3)
mat

##         [,1]     [,2]      [,3]     [,4]
## [1,] -1.9144 -0.46353  2.087167 -1.64061
## [2,]  1.1766 -1.11592  0.017396  0.45019
## [3,] -1.6650 -0.75082 -1.286301 -0.01856

apply(X = mat, MARGIN = 1,FUN = "sum") # applica a mat per righe la somma

## [1] -1.93133  0.52825 -3.72065

apply(X = mat, MARGIN = 2,FUN = "mean") # applica a mat per colonne la media

## [1] -0.80092 -0.77676  0.27275 -0.40299

tapply applica una funzione solo su elementi che rispettano una condizione

sesso <- c("M","M","M","F","F")
eta   <- c(32.2,45.6,65.3,34.1,43.2)
tapply(eta, sesso, median) # applica la mediana al gruppo M e al gruppo F

##     F     M 
## 38.65 45.60

Le funzioni lapplay e sapply (versione semplificata delle prima) applicano una funzione ad una lista o agli elementi di un vettore

gruppo1 <- rnorm(5,9.4,1.1)  # gruppo1 5 estrazioni da una N( 9.4,1.1^2)
gruppo2 <- rnorm(9,12.2,1.2) # gruppo2 9 estrazioni da una N(12.2,1.2^2)
gruppo3 <- rnorm(7,11.7,0.9) # gruppo3 7 estrazioni da una N(11.7,0.9^2)
campione <- list(gruppo1,gruppo2,gruppo3)
# applica media e varianza ad ogni gruppo:
lapply(campione,FUN = function(x)c(mean(x),var(x))) 

## [[1]]
## [1] 8.7818 1.1357
## 
## [[2]]
## [1] 12.6776  2.1178
## 
## [[3]]
## [1] 11.8613  1.0098

sapply(campione,FUN = function(x)c(mean(x),var(x))) # come sopra ma in matrice

##        [,1]    [,2]    [,3]
## [1,] 8.7818 12.6776 11.8613
## [2,] 1.1357  2.1178  1.0098

Funzioni personalizzate

Le funzioni si possono creare con la funzione function

funz1 <- function(x) x^2 # funz1 usa x come input e x^2 come output
funz1(3)

## [1] 9

funz2 <- function(x,y) { # funz2 usa x e y come input 
  risultato <- ifelse(x>y,x+y,"x deve essere maggiore di y!")
  return(risultato)
} 
funz2(2,3)

## [1] "x deve essere maggiore di y!"

funz2(3,1)

## [1] 4

Possiamo per esempio creare la funzione che crei la varianza del campione e la SD non corretta

var_pop <- function(x) {
  vpop <- mean(x^2)-mean(x)^2 # media dei quadrati meno il quadrato della media
  return(vpop)  
}
n <- 10
x <- rnorm(n,mean = 10,sd = 1)
var(x)     # varianza corretta

## [1] 0.88378

var_pop(x) # varianza NON corretta

## [1] 0.7954

n/(n-1)*var_pop(x) # correzione

## [1] 0.88378

sd_pop <- function(x) sqrt(var_pop(x)) # rad. quad. della varianza 
sd_pop(x)

## [1] 0.89185

Possiamo anche creare una funzione che calcola un intervallo di confidenza al livello \(1-\alpha\), per un \(\alpha\) qualunque

## intervallo di confidenza per mu, sigma nota

idc_mu <- function(mu_obs,sigma,alpha=0.05){
z_alpha <- qnorm(1-alpha/2) # fisso z_alpha
SE      <- sigma/sqrt(n) # SE per mu = sigma diviso radice di n

cat("L'intervallo di confidenza al ",(1-alpha)*100,"% è dato da \n",
    "[",mu_obs," - ",z_alpha," x ",SE," ; ",mu_obs," + ",z_alpha," x ",SE,"] \n",
    "[",mu_obs-z_alpha*SE," ; ",mu_obs+z_alpha*SE,"]",
    sep="")
}

alpha   <- 0.01     # fisso alpha
mu_obs  <- 23.3     # fisso la media del campione
sigma   <- 2.13     # fisso il sigma di popolazione
n       <- 34       # fisso n

idc_mu(mu_obs = mu_obs, sigma = sigma, alpha = alpha)

## L'intervallo di confidenza al 99% è dato da 
## [23.3 - 2.5758 x 0.36529 ; 23.3 + 2.5758 x 0.36529] 
## [22.359 ; 24.241]

[1] R Core Team (2022). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/.

[2] JJ Allaire and Yihui Xie and Jonathan McPherson and Javier Luraschi and Kevin Ushey and Aron Atkins and Hadley Wickham and Joe Cheng and Winston Chang and Richard Iannone (2022). rmarkdown: Dynamic Documents for R. R package version 2.14. URL https://rmarkdown.rstudio.com.

[3] Yihui Xie and J.J. Allaire and Garrett Grolemund (2018). R Markdown: The Definitive Guide. Chapman and Hall/CRC. ISBN 9781138359338. URL https://bookdown.org/yihui/rmarkdown.

[4] Yihui Xie and Christophe Dervieux and Emily Riederer (2020). R Markdown Cookbook. Chapman and Hall/CRC. ISBN 9780367563837. URL https://bookdown.org/yihui/rmarkdown-cookbook.